Question 70349This question is from textbook Algebra & Trigonometry with Geometry
: This is the last of my quiz questions that I am using to prep for my final exam.
For the function defined by f(x)=5x-4, find a formula for f-^1(x).
Solve the equation 4^(2x)+1 = 2^(3x)+6 ?
Find an exponential function of the form f(x)=ba^x+c with y-intercept 2, horizontal asymptote y=-2, that passes through the point P(1,4).
Solve the equation (f o g)^-1(3)?
For the function defined by f(x)=2-x^2, 0 < (underlined) x, use a sketch to help find a formula for f-^1(x).
The amount of a radioactive tracer remaining after t days is given by A=Ao e^-0.058t, where Ao is the starting amount at the beginning of the time period. How many days will it take for one half of the original amount to decay?
The population P of a certain culture is expected to be given by a model P=100e^rt where r is a constant to be determined and t is a number of days since the original population of 100 was established. Find the value of r if the population is expected to reach 200 in 3 days.
Please help! My exam is on Friday.
Thanks, John
This question is from textbook Algebra & Trigonometry with Geometry
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website! For the function defined by f(x)=5x-4, find a formula for f-^1(x).
 Replace
Replace  by by 
 Interchange x and y
Interchange x and y
 Solve for y
Solve for y


 Replace
Replace  by by 
 -------------------------------
Solve the equation 4^(2x+1) = 2^(3x+6) ?
-------------------------------
Solve the equation 4^(2x+1) = 2^(3x+6) ?
 Write
Write  as as 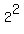
 Simplify the left side
Simplify the left side

 Now use the principle that if two powers of the same
positive base are equal, and the base is not 1, then
the exponents must be equal:
Now use the principle that if two powers of the same
positive base are equal, and the base is not 1, then
the exponents must be equal:

 ----------------------------------------
Find an exponential function of the form
----------------------------------------
Find an exponential function of the form  with
y-intercept 2, horizontal asymptote y=-2, that passes through the
point P(1,4).
The graph of with
y-intercept 2, horizontal asymptote y=-2, that passes through the
point P(1,4).
The graph of  has horizontal asymptote y = 0, the
x-axis. To move that asymptote down to y=-2 we must shift the graph
downward by 2 units, so we add -2 to the right side, which makes
c = -2
So far we have has horizontal asymptote y = 0, the
x-axis. To move that asymptote down to y=-2 we must shift the graph
downward by 2 units, so we add -2 to the right side, which makes
c = -2
So far we have  To have y-intercept 2, it must pass through the point (0,2)
so that f(0) = 2.
To have y-intercept 2, it must pass through the point (0,2)
so that f(0) = 2.



 So far we have
So far we have  To pass through the point (1,4) we have f(1) = 4.
To pass through the point (1,4) we have f(1) = 4.



 So we have
So we have 
 -------------------------------------------------
Solve the equation (f o g)^-1(3)?
You didn't give f(x) and g(x), so I can't do that one
without that information.
-------------------------------------------------
For the function defined by
-------------------------------------------------
Solve the equation (f o g)^-1(3)?
You didn't give f(x) and g(x), so I can't do that one
without that information.
-------------------------------------------------
For the function defined by  , ,  , use
a sketch to help find a formula for , use
a sketch to help find a formula for  .
First we sketch the graph of .
First we sketch the graph of  , , 
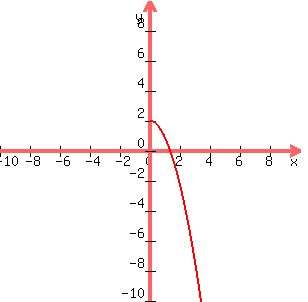 Now we draw in the identity line whose equation is
Now we draw in the identity line whose equation is 
 Now we draw the curve reflecting it into the identity line and we
get the
Now we draw the curve reflecting it into the identity line and we
get the
 The blue curve is the graph of
The blue curve is the graph of  To find an equation for
To find an equation for  we proceed as in the
first problem above we proceed as in the
first problem above
 Replace
Replace  by by 
 Interchange x and y
Interchange x and y
 Solve for y
Solve for y

 =± =±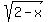 We can see from the graph that the blue curve is above the
x-axis so we ignore the - solution
Replace
We can see from the graph that the blue curve is above the
x-axis so we ignore the - solution
Replace  by by 
 -----------------------------------------
The amount of a radioactive tracer remaining after t days is given by
A = A0e-0.058t, where A0 is the
starting amount at the beginning of the time period. How many days
will it take for one half of the original amount to decay?
This is when A = A0/2
So substitute A0/2 for A
A0/2 = A0e-0.058t
Divide both sides by A0
1/2 = e-0.058t
Use principle that X = eY can be written as Y = ln(X)
to rewrite that as
-0.058t = ln(1/2)
t = ln(1/2)/(-0.058) = 11.95081346 days or about 12 days.
-----------------------------------------------
The population P of a certain culture is expected to be given by
a model P=100ert where r is a constant to be determined
and t is a number of days since the original population of 100 was
established. Find the value of r if the population is expected to
reach 200 in 3 days.
Substitute 200 for P and 3 for t
P = 100ert
200 = 100er·3
200 = 100e3r
Divide both sides by 100
2 = e3r
Use principle that X = eY can be written as Y = ln(X)
to rewrite that as
3r = ln(2)
r = ln(2)/3 = .2310490602
Edwin
-----------------------------------------
The amount of a radioactive tracer remaining after t days is given by
A = A0e-0.058t, where A0 is the
starting amount at the beginning of the time period. How many days
will it take for one half of the original amount to decay?
This is when A = A0/2
So substitute A0/2 for A
A0/2 = A0e-0.058t
Divide both sides by A0
1/2 = e-0.058t
Use principle that X = eY can be written as Y = ln(X)
to rewrite that as
-0.058t = ln(1/2)
t = ln(1/2)/(-0.058) = 11.95081346 days or about 12 days.
-----------------------------------------------
The population P of a certain culture is expected to be given by
a model P=100ert where r is a constant to be determined
and t is a number of days since the original population of 100 was
established. Find the value of r if the population is expected to
reach 200 in 3 days.
Substitute 200 for P and 3 for t
P = 100ert
200 = 100er·3
200 = 100e3r
Divide both sides by 100
2 = e3r
Use principle that X = eY can be written as Y = ln(X)
to rewrite that as
3r = ln(2)
r = ln(2)/3 = .2310490602
Edwin
|
|
|