SOLUTION: what binomial of lowest degree must be multiplied to x3-3x2-9x-5 to make it a polynomial with perfect root?

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: what binomial of lowest degree must be multiplied to x3-3x2-9x-5 to make it a polynomial with perfect root?       Log On


   

Question 703190: what binomial of lowest degree must be multiplied to x3-3x2-9x-5 to make it a polynomial with perfect root?
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
The possible rational roots for P%28x%29=x%5E3-3x%5E2-9x-5 are 1, -1, 5, and -5.
P%28-1%29=%28-1%29%5E3-3%28-1%29%5E2-9%28-1%29-5=-1-3%2B9-5=0,
so -1 is a root of P%28x%29 and
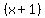P%28x%29 has %28x%2B1%29 as a factor.
Using division (long or synthetic) you find that
P%28x%29=%28x%5E2-4x-5%29%28x%2B1%29
Factoring further, since x%5E2-4x-5=%28x-5%29%28x%2B1%29 , you find that
P%28x%29=%28x-5%29%28x%2B1%29%28x%2B1%29
So, multiplying times 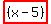highlight%28%28x-5%29%29 , you would get the perfect square


NOTE: I do not like to divide polynomials, so I factor by grouping, like this:

(It's also too difficult for me to get terms/coefficients to line up when typing stuff into this website).