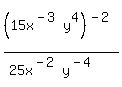We want to remove the parentheses in the top.
Let's first make sure every factor inside the
parentheses shows its exponent. That is, give
the 15 an exponent of 1:
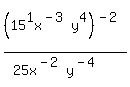Remove the parentheses on top by distributing
exponents. That is, by multiplying each exponent
inside the parentheses by the exponent outside
the parentheses on the right:
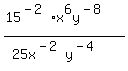Next we make each factor with a negative exponent
have a positive exponent by bringing from numerator
to denominator or from denominator to numerator.
I'll do them one at a time, but you can do them all in
one step.
Move the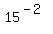 
from the top to the bottom as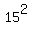 
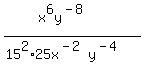Move the 
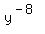from the top to the bottom as 
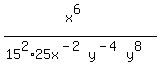Move the 
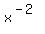from the bottom to the top as 
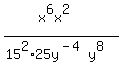Move the 
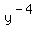from the bottom to the top as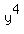 
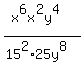Now we have only positive exponents.
Add the exponents of x in the top, getting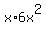 
as 
:
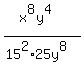Subtract the exponents of the y's.
Use the rule: Subtract them "largest
minus smallest, and put the result
where the LARGER exponent was before
subtracting. So we subtract exponents
of the y's as 8-4 or 4 and put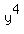
in the bottom because that's where the
larger exponent of y was in the last step:
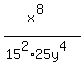Finally we multiply the 
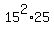out as 5625,
and the final answer is:
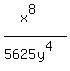Edwin
