Question 701683: I have a 30-60-90 triangle, and the long leg is 33 degrees. How do I find the short leg and hypotenuse?
Found 2 solutions by MathLover1, MathTherapy:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A 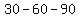 triangle is a right triangle whose internal angles are triangle is a right triangle whose internal angles are  , ,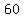 and and 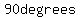 . .
The three sides of a 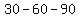 triangle have the following characteristics: triangle have the following characteristics:
All three sides have 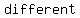 lengths. lengths.
The shorter leg, , is half the length of the hypotenuse, , is half the length of the hypotenuse,  . That is, . That is,

The longer leg's length,  , is the shorter leg times , is the shorter leg times  . That is, . That is,

so, you are given 
then, you have the shorter leg  ...=>... ...=>... ...=>... ...=>...
and the longer leg's length is  ..=>... ..=>... ...=>... ...=>...
check result using Pythagorean theorem:



 ...round decimal to whole number ...round decimal to whole number

Answer by MathTherapy(10552)   (Show Source): (Show Source):
|
|
|