Question 701614: a(subscript 1) = 28, a(subscript k=1) = a(subscript k) - 4
Please tell me what these numbers indicate and help me solve this
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! You may have seen  , , 
A sequence of numbers increasing (or decreasing) from one to the next
by the same difference is called an "arithmetic sequence"
or an "arithmetic progression".
Each number in the sequence is called a "term".
It is considered that each term in an arithmetic sequence,
is equal to the previous term PLUS a "common difference,"
usually represented by  . .
So if each term was 4 less than the previous one,
the common difference would be  . .
Usually, the first term is represented by  , ,
the second term is represented by  , ,
the term number  is represented by is represented by 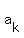 , ,
and the term number 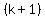 is represented by is represented by 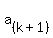 . .
To define a never ending sequence, with infinite terms,
a formula is given.
The formula  gives you the sequence of the odd integers: gives you the sequence of the odd integers:
1, 3, 5, 7, .....
Otherwise you could be given the value of one term,
and the formula to calculate each term from the one before,
such as  , that says that to get the next term, you subtract , that says that to get the next term, you subtract  . .
So, if  , ,
 , ,
 , ,
 , ,
 , ,
and so on.
By the time you get to term number  , ,
you have subtracted  a total of a total of 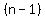 times, times,
and 
|
|
|