|
Question 701011: Can someone please help me. I don't understand how to start these.
1. For the given equation, list the intercepts and test for symmetry.
y=x^2-5x-6
2. Write the equation of the circle in standard form. Find the center, radius, intercepts, and graph the
circle.
x^2+y^2+14x-12y=-76
Found 2 solutions by MathLover1, KMST:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1.

the intercepts:
set  and find and find 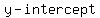

 ....... .......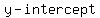 is at ( is at ( , , ) )
set  and find and find 
 .....use quadratic formula .....use quadratic formula
 ...in your case ...in your case  , ,  , and , and 




solutions:


 .......one .......one 
and


 .......another .......another 
so,  are at ( are at ( , , ) and ( ) and ( , , ) )
graph:

parabola has an axis of symmetry which is the line that runs down its 'center' or vertex
since your equation is in standard form, then the formula for the axis of symmetry is:
 from the general standard form equation from the general standard form equation 
so, plug in  and and 


 ....so,axis of symmetry is a line parallel to ....so,axis of symmetry is a line parallel to  and crosses and crosses  at point ( at point ( , , ) )
let's see it on a graph:

2.

 ......write ......write  as as 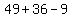
 ...group ...group 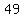 with with 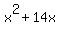 , and , and  with with 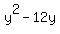
 ...recognize square of the sum for ...recognize square of the sum for  part and square of the difference for part and square of the difference for  part part
 .....move .....move  to the right to the right
 .........your answer for the equation of the circle in standard form .........your answer for the equation of the circle in standard form 
as you can see  and and  , so the center is at ( , so the center is at ( , , ) )
radius is 
intercepts:
set  and find and find 




 .......use quadratic formula .......use quadratic formula




 ....as you can see, solution is complex, and it means there are ....as you can see, solution is complex, and it means there are  
set  and find and find 



 .......use quadratic formula .......use quadratic formula




 ...solution is complex, and it means there are ...solution is complex, and it means there are  
and graph of the circle:

Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1.  can be called a quadratic function and graphs as a parabola opening up. (It's shaped like a smile). can be called a quadratic function and graphs as a parabola opening up. (It's shaped like a smile).
Intercepts are the points where the graph representing that equation crosses the x-axis and the y-axis.
The x-axis is the set of all the points with  . .
Making  we find the x-intercepts: we find the x-intercepts:
 --> -->  (factoring) (factoring)
has a solution when  --> -->  and and
a solution when  --> --> 
The y-axis is the set of all the points with  . .
Making  we find the y-intercept: we find the y-intercept:
 --> -->  --> --> 
When teachers say to test for SYMMETRY they usually want you to find out, without graphing,
if the graph representing the equation has symmetry.
Maybe the side to the right of the y-axis is a mirror image of the left side.
Or maybe the side above of the x-axis is a mirror image of side below the x-axis.
Or maybe every point has a reflection on the other side of the origin.
To find out, you change  to to  , ,
or  to to 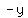 , ,
or (x,y) to (-x,-y),
and see if you end up with the same equation.
For  , any of those changes gives you a different equation. , any of those changes gives you a different equation.
The graph for  has an axis of symmetry, but it is neither the x-axis, not the y-axis. has an axis of symmetry, but it is neither the x-axis, not the y-axis.
Knowing that a graph will be symmetrical before you start graphing, makes graphing easier.
In pictures,
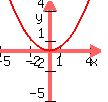 is a function with symmetry about the y-axis because it has the same y for is a function with symmetry about the y-axis because it has the same y for  and and  ( f(x)=f(-x) } ( f(x)=f(-x) }
 graphs as graphs as  and has symmetry about the x-axis, because for and has symmetry about the x-axis, because for  and for and for 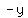 the equation is the same. the equation is the same.
  and and  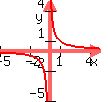
have symmetry about the origin because the equation is the same for point (x,y) as for point (-x,-y).
2.  --> -->  --> -->  --> -->  --> --> 
That equation is true for all the points (x,y) that are at distance 3 from point (-7,6).
That is the equation of a circle with radius 3, centered at the point (-7,6),
with  and and  . .
The center is too far below the x-axis compared to the radius, so the circle does not cross the x-axis, and there are no x-intercepts.
The same thing happens with the y-axis. The center is too far to the right. There is no y-intercept.
|
|
|
| |