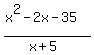Translates to
____________
x+5 |x^2-2x-35
The first division occurs between the x^2 and the x. The question is: how many times does x go into x^2? The answer is x times (in other words x*x=x^2) so the first part of the quotient is x
_x___________
x+5 |x^2-2x-35
Now multiply x by (x+5) and place the product directly under x^2-2x-35
_x___________
x+5 |x^2-2x-35
-(x^2+5x)<---------remember the negative distributes
So subtract (x^2+5x) from x^2-2x-35 and you get 0x^2-7x
_x___________
x+5 |x^2-2x-35
-(x^2+5x)
----------
0x^2-7x
Now the question is: how many times does x+5 go into -7x? The answer is -7 (x*(-7)=-7x)
_x__-7________
x+5 |x^2-2x-35
-(x^2+5x)
----------
0x^2-7x-35<---------remember to pull down another part of the dividend
Multiply -7 by (x+5) to get -7x-35 and place it under -7x-35
_x__-7________
x+5 |x^2-2x-35
-(x^2+5x)
----------
0x^2-7x-35
-(7x-35)
--------
0
So your answer is (x-7).
To verify you can multiply (x-7) by (x+5)
check: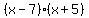 
FOIL these factors
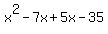
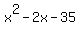this verifies our answer
If you want to compute this answer quickly to check your work, check out http://www.calc101.com/webMathematica/long-divide.jsp. This page has a polynomial division calculator that allows you to do this quickly and shows its steps.
(