SOLUTION: write a polynomial function of least degree with integral coefficients having roots ( -4-2i) and -2/3

Algebra ->  Rational-functions -> SOLUTION: write a polynomial function of least degree with integral coefficients having roots ( -4-2i) and -2/3      Log On


   

Question 699415: write a polynomial function of least degree with integral coefficients having roots ( -4-2i) and -2/3
Answer by josgarithmetic(39620) About Me  (Show Source):
You can put this solution on YOUR website!
Those are two roots. One of them is a complex root and such type of roots for polynomial functions occur in conjugate pairs. The required function will have then, three roots: -4-2i, -4+2i, and -2/3. The binomials which would match those roots can be (x-(4+2i)), (x-(4-2i)), and (x-(-2/3)).

Those are equivalent to when multiplied:
**,y=%28x%5E2-8x%2B20%29%28x%2B2%2F3%29

If you have no trouble with the multiplication, then I'll leave off the steps. If my solution was done properly, the (x-(4+2i))*(x-(4-2i)) should be (x^2-8x+20).

**, In fact, I believe I made a mistake. Difficult to trace, but the quadratic factor should be 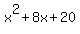x%5E2%2B8x%2B20.