Question 699054: A regular hexagon has an area of 45 sqrt3 . What is its perimeter? Please explain step by step
Answer by Positive_EV(69)   (Show Source): (Show Source):
You can put this solution on YOUR website! A regular hexagon can be divided into six equilateral triangles with the same area and with a side length equal to the length of the side of the hexagon. Each of these triangles will have an area of 1/6th that of the hexagon, which is  . .
There's a few ways to find the side of an equilateral triangle given its area, but I'll use Hero's formula. Hero's formula says that the area of a triangle with sides a, b, and c is equal to
 , where s = (1/2)*(a+b+c). For an equilateral triangle, a = b = c, so I will refer to the length of a side as a, and s = (1/2)(a+a+a) = (3/2)a. Hero's formula becomes: , where s = (1/2)*(a+b+c). For an equilateral triangle, a = b = c, so I will refer to the length of a side as a, and s = (1/2)(a+a+a) = (3/2)a. Hero's formula becomes:





The perimeter is 6 times the length of a side, or 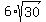 . .
Alternatively, you can find the side length of the triangle by using the A = (1/2)*base*height formula by drawing the height and noting that two 30-60-90 triangles are formed. The height of the triangle is going to be  times the length of a side, so you can also use times the length of a side, so you can also use
 , which gives the same value of , which gives the same value of 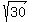 for a and for a and 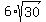 for the perimeter. for the perimeter.
|
|
|