Ellipses like this  have equations of this form with aČ under the term in x
have equations of this form with aČ under the term in x




 Ellipses like this
Ellipses like this  have equations of this form with aČ under the term in y
have equations of this form with aČ under the term in y
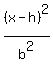

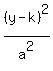

 a is always greater than b, and of course aČ is greater than bČ.
a is always greater than b, and of course aČ is greater than bČ.
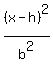

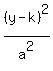

 The center is (h,k), the semi-major axis is a, the semi minor axis is b.
The center is (h,k), the semi-major axis is a, the semi minor axis is b.
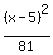



 Since the denominator 81 is larger than the denominator 25, so we know
this is an ellipse that looks like this
Since the denominator 81 is larger than the denominator 25, so we know
this is an ellipse that looks like this  By comparison h=5, k=9, aČ=81, bČ=25, and so a=9, b=5
So the center is (h,k) = (5,9). The major axis is 2a=18, and the minor
axis is 2b=10, and the two axes bisect each other at the center (5,9),
so we draw this:
By comparison h=5, k=9, aČ=81, bČ=25, and so a=9, b=5
So the center is (h,k) = (5,9). The major axis is 2a=18, and the minor
axis is 2b=10, and the two axes bisect each other at the center (5,9),
so we draw this:


 Edwin
Edwin