Question 698899: can you help me solve substitution problems. if you dont mind help me solve for x ill just solve for y. 1. 3x+y=25 x=y+3 2. 3x-2y=7 x+3y=-5
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I'll find  (For those particular systems, it's easier that way). (For those particular systems, it's easier that way).
Then you can solve for  . .
Not all systems lend themselves to an easy resolution by substitution.
Substitution is easiest when you have one equation in the form y=___ or x=___ ,
with a simple expression to the right of the equal sign.
If you can transform one equation into that form and end with an easy expression, it would work too.
That happens when one of the variables does not have a coefficient in front of it,
like the  in in  . .
The wise student will chose the easiest way to solve a system,
because complicated ways increase the risk of making dumb mistakes.
1) 
In this case, you already have  in the right form. in the right form.
That equations tells you that the expression 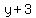 is equal to is equal to  , ,
so I just substitute the expression 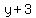 for for  in the other equation to get in the other equation to get
 that I can solve for that I can solve for 
 --> -->  --> -->  --> -->  --> -->  --> -->  --> --> 
At this point, I would substitute  for for  in the equation that will make finding in the equation that will make finding  easier: easier:  . .
2) 
The easiest way to transform one of those equation so that one variable is isolated on one side of the equal sign is

That is a wise choice, that gives me a simple expression for  . .
Substituting 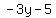 for for  in in  , I get , I get
 , which I will solve for , which I will solve for 
 --> -->  --> -->  --> -->  --> -->  --> -->  --> -->  . .
At this point, I would substitute  for for  in the equation that will make finding in the equation that will make finding  easier. easier.
Maybe I would use  . .
NOTE:
A different choice could have complicated my work.
If I decided to solve  for for  , I would do , I would do
 --> -->  --> -->  --> -->  . .
That expression for  has fractions, and will make me likely to make a silly mistake. has fractions, and will make me likely to make a silly mistake.
It is sad to lose grade points (and time),
just because of complicated expressions that lead to silly mistakes,
especially when you really know your algebra.
Next, I would be substituting 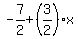 for for  in in 
(In doing the calculations above,
I made a mistake with the sign of one of those fractions,
and I only noticed because I had solved the system the easier way before,
and had found  . .
I had to review carefully to see where I had messed up, and to correct it).
|
|
|