SOLUTION: write the equation of the ellipse 4x^2+9y^2-64x+162y+949=0 in standard form.

4x² + 9y² - 64x + 162y + 949 = 0

We want to get it in one of these forms:

 or  

4x² + 9y² - 64x + 162y + 949 = 0

Swap the second and third terms to get the y-terms 
together and the x terms together.  Also add -949 
to both sides:

      4x² - 64x + 9y² + 162y = -949 

Factor just the 4 out of the first two terms on the 
left, and just the 9 out of the last two terms on
the left:

   4(x² - 16x) + 9(y² + 18y) = -949

We find what numbers we must add inside
those parentheses to complete the square.

Multiply the coefficient of x in the first parentheses,
which is -16 by.  Get -8.  The square that and
get (-8)² = +64.  That's what we add inside the first 
parentheses.

Multiply the coefficient of y in the second parentheses,
which is 18 by.  Get 9.  The square that and
get 9² = +81.  That's what we add inside the second 
parentheses.

   4(x² - 16x + 64) + 9(y² + 18y + 81) = -949 + 256 + 729

Notice that we added 256 on the right because when +64 
is added inside the first parentheses, since there is a 4
coefficient before the entire first parentheses, it really 
amounts to adding 4×64 or 256 to the left side, so we have 
to do the same to the right side.

Notice also that we added 729 on the right because when +81 
is added inside the second parentheses, since there is a 9
coefficient before the entire first parentheses, it really 
amounts to adding 9×81 or 729 to the left side, so we have 
to do the same to the right side.

Now we factor the two parentheses and combine the terms on
the right side:

     4(x - 8)(x - 8) + 9(y + 9)(y + 9) = 36

                 4(x - 8)² + 9(y + 9)² = 36

Divide through by 36 to get 1 on the right:

                  +  = 
               
                  +  = 

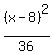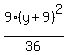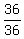
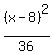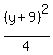That's the form  

where (h,k) = (8,-9), a = 6, b = 2 and so the graph is

        

Edwin