|
Question 698810: write the equation of the ellipse 4x^2+9y^2-64x+162y+949=0 in standard form.
Found 2 solutions by MathLover1, Edwin McCravy:
Answer by MathLover1(20850)   (Show Source): (Show Source):
Answer by Edwin McCravy(20064)   (Show Source): (Show Source):
You can put this solution on YOUR website!
4x² + 9y² - 64x + 162y + 949 = 0
We want to get it in one of these forms:
 or or  4x² + 9y² - 64x + 162y + 949 = 0
Swap the second and third terms to get the y-terms
together and the x terms together. Also add -949
to both sides:
4x² - 64x + 9y² + 162y = -949
Factor just the 4 out of the first two terms on the
left, and just the 9 out of the last two terms on
the left:
4(x² - 16x) + 9(y² + 18y) = -949
We find what numbers we must add inside
those parentheses to complete the square.
Multiply the coefficient of x in the first parentheses,
which is -16 by
4x² + 9y² - 64x + 162y + 949 = 0
Swap the second and third terms to get the y-terms
together and the x terms together. Also add -949
to both sides:
4x² - 64x + 9y² + 162y = -949
Factor just the 4 out of the first two terms on the
left, and just the 9 out of the last two terms on
the left:
4(x² - 16x) + 9(y² + 18y) = -949
We find what numbers we must add inside
those parentheses to complete the square.
Multiply the coefficient of x in the first parentheses,
which is -16 by . Get -8. The square that and
get (-8)² = +64. That's what we add inside the first
parentheses.
Multiply the coefficient of y in the second parentheses,
which is 18 by . Get -8. The square that and
get (-8)² = +64. That's what we add inside the first
parentheses.
Multiply the coefficient of y in the second parentheses,
which is 18 by . Get 9. The square that and
get 9² = +81. That's what we add inside the second
parentheses.
4(x² - 16x + 64) + 9(y² + 18y + 81) = -949 + 256 + 729
Notice that we added 256 on the right because when +64
is added inside the first parentheses, since there is a 4
coefficient before the entire first parentheses, it really
amounts to adding 4×64 or 256 to the left side, so we have
to do the same to the right side.
Notice also that we added 729 on the right because when +81
is added inside the second parentheses, since there is a 9
coefficient before the entire first parentheses, it really
amounts to adding 9×81 or 729 to the left side, so we have
to do the same to the right side.
Now we factor the two parentheses and combine the terms on
the right side:
4(x - 8)(x - 8) + 9(y + 9)(y + 9) = 36
4(x - 8)² + 9(y + 9)² = 36
Divide through by 36 to get 1 on the right: . Get 9. The square that and
get 9² = +81. That's what we add inside the second
parentheses.
4(x² - 16x + 64) + 9(y² + 18y + 81) = -949 + 256 + 729
Notice that we added 256 on the right because when +64
is added inside the first parentheses, since there is a 4
coefficient before the entire first parentheses, it really
amounts to adding 4×64 or 256 to the left side, so we have
to do the same to the right side.
Notice also that we added 729 on the right because when +81
is added inside the second parentheses, since there is a 9
coefficient before the entire first parentheses, it really
amounts to adding 9×81 or 729 to the left side, so we have
to do the same to the right side.
Now we factor the two parentheses and combine the terms on
the right side:
4(x - 8)(x - 8) + 9(y + 9)(y + 9) = 36
4(x - 8)² + 9(y + 9)² = 36
Divide through by 36 to get 1 on the right:
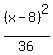 + + 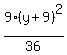 = = 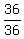
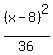 + + 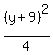 = =  That's the form
That's the form  where (h,k) = (8,-9), a = 6, b = 2 and so the graph is
where (h,k) = (8,-9), a = 6, b = 2 and so the graph is
 Edwin
Edwin
|
|
|
| |