a) How many groups would you expect to have all three balls painted the same color?
There will be 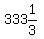 groups.
The expected number of three of the same color is np where n=
groups.
The expected number of three of the same color is np where n=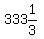 and p is
the probability of choosing 3 balls painted the same color.
Actually to find the probability of choosing 3 we would be choosing without
replacement. However, since there are 1000 balls, the probability of choosing
without replacement is approximately the same as choosing with replacement.
So the probability of selecting 3 reds is
P[(red 1st) AND (red 2nd) AND (red 3rd) = approximately
and p is
the probability of choosing 3 balls painted the same color.
Actually to find the probability of choosing 3 we would be choosing without
replacement. However, since there are 1000 balls, the probability of choosing
without replacement is approximately the same as choosing with replacement.
So the probability of selecting 3 reds is
P[(red 1st) AND (red 2nd) AND (red 3rd) = approximately 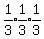 =
= 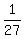 .
and the probabilities of choosing 3 greens and of 3 blues are the same. So the
probability of selecting 3 of the same color is
.
and the probabilities of choosing 3 greens and of 3 blues are the same. So the
probability of selecting 3 of the same color is 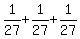 =
=  =
=  .
So the expected number is
.
So the expected number is 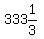 groups times
groups times  or about 37.04
-----------
or about 37.04
-----------
b) If your blue can was 75% empty and only had enough paint to cover 200 balls, how many groups would you expect to have 3 red balls?
On the average when the first 600 have been painted,  of them,
or 200 will be red, 200 will be green and 200 will be blue.
But now we're out of blue paint, so on the average, half the
remaining 400, or 200, will be red and the other 200 green.
So on the average we end up with 400 reds, 400 greens, and 200 blues.
The expected number of three reds is np where and n =
of them,
or 200 will be red, 200 will be green and 200 will be blue.
But now we're out of blue paint, so on the average, half the
remaining 400, or 200, will be red and the other 200 green.
So on the average we end up with 400 reds, 400 greens, and 200 blues.
The expected number of three reds is np where and n = 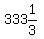 and p is the probability of selecting 3 reds.
Again since there are 1000 balls, the probability of choosing without
replacement is approximately the same as choosing with replacement.
The probability of selecting a red ball is
and p is the probability of selecting 3 reds.
Again since there are 1000 balls, the probability of choosing without
replacement is approximately the same as choosing with replacement.
The probability of selecting a red ball is 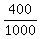 =
=  P[(red 1st) AND (red 2nd) AND (red 3rd)] = approximately
P[(red 1st) AND (red 2nd) AND (red 3rd)] = approximately  =
=  .
So the expected number is
.
So the expected number is 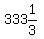 groups times
groups times  or about 21.33.
Edwin
or about 21.33.
Edwin