SOLUTION: this is just a simple algebra problem but I'm confused about how PEMDAS would work on this. the problem is 6/2(1+2) (the "/" meaning divide). I worked the parentheses first, 6/

Algebra ->  Expressions -> SOLUTION: this is just a simple algebra problem but I'm confused about how PEMDAS would work on this. the problem is 6/2(1+2) (the "/" meaning divide). I worked the parentheses first, 6/      Log On


   

Question 698291: this is just a simple algebra problem but I'm confused about how PEMDAS would work on this. the problem is 6/2(1+2) (the "/" meaning divide). I worked the parentheses first, 6/2(3). now....do I multiply the 2 to the 3 in parentheses? or do the division then multiply?
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
6/2(1+2) = 6/2(3)=3(3) = 9
Division has the same higher priority as multiplication (and subtraction has the same priority as addition).
When you are writing stuff like 6/2(1+2) with all the numbers in one horizontal line you go from left to right, and do multiplications and divisions as you go (same with adding and subtracting).
4(1+1)+15/5-12/6(2)+(3-1)-5 = 4(2)+3-2(2)+2-5 = 8+3-4+2-5 = 8-4+2-5 = 4+2-5 = 6-5=1

NOTE: If you've learned about writing math in more than one line,
for expressions like 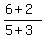%286%2B2%29%2F%285%2B3%29,
you work on each side of the line separately
%286%2B2%29%2F%285%2B3%29=8%2F8=1.
And if you cannot write that in two lines, because you are typing,
you need to add parentheses:
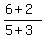%286%2B2%29%2F%285%2B3%29 = (6+2)/(5+3)

Division has the same higher priority as multiplication (and subtraction has the same priority as addition).
It could be stated as PEMDAS = PEDMSA, but PEDMSA is hard to pronounce.
Some teach it as PE(MD)AS, or as PEmatrix%282%2C1%2CM%2CD%29matrix%282%2C1%2CA%2CS%29.

I think of it as PEMA, because I do not believe in division or subtraction.
There is only multiplication and addition (but your numbers include negative and fractional numbers).
If you had not been brainwashed at a very early age to believe in division and subtraction, algebra would be easier.
Dividing is really multiplying by the reciprocal.
I see 6/2(3) as 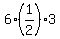6%281%2F2%293 or 6%2F2%2A3.
Subtracting is really adding the opposite.
I write 8+3-4+2-5 (because it's easier, but I see 8+3-4+2-5 as 8 + 3 +(-4) + 2 +(-5), and I really see it as a bunch of numbers to be added in any order.