Question 697930: How do you graph equations? my problem is y= (-1) and my teacher gave me a piece of grid paper but I don't understand how to do it.
Found 2 solutions by stanbon, josmiceli:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! How do you graph equations? my problem is y= (-1) and my teacher gave me a piece of grid paper but I don't understand how to do it.
-------
Draw a set of axes on the grid paper.
Plot a few points and plot each point on the x/y system.
Let x = -2 ; y = -1 gives you point (-2,-1)
Let x = 0 ; y = -1 gives you point (0,-1)
Let x = 2 ; y = -1 gives you point (2,-1)
------------
Draw a line thru the points.
You should see a horizontal line passing thru all the
points where y = -1.
=========
Cheers,
Stan H.
===========
Answer by josmiceli(19441)   (Show Source): (Show Source):
You can put this solution on YOUR website! The idea behind graphing is that no matter where you are
on a plane surface, all you need is 2 numbers in order
to tell someone where you are.
Suppose you are on a flat plane with nothing in sight to
use as a description of where you are. Then you notice there are
2 straight lines intersecting at right angles that extend to
infinity.
Now all you have to do is measure your distance, (a) from one line
( call it the y-axis ), then measure your distance, (b) from the
other line ( call it the x-axis ). Now your position is:
( x[1] , y[1] ) = ( a , b )
where a and b are the measurements you made.
-----------------------------------------
Now your problem is to really understand what 
means. I just told you that you needed 2 measurements to
locate a point on a plane, so this can't be a point.
What it is is a line, but this line always sees 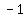 when when
it looks at the y-axis, but it can see anything when it looks at the x-axis.
So this is the line  which is parallel to the x-axis which is parallel to the x-axis
and intersects the y-axis at the point (0,-1).
So if you pick a point at random on this line, you see a random point on the x-axis,
but you see 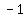 on the y-axis on the y-axis
--------------
Hope all this helps. It wasn't easy for me, and the
only way to fully get it is to just keep working
problems or comprehension exercises.
|
|
|