|
Question 697781: A cable suspended form supports that are the same height and 600ft apart has a sag of 200ft. If the cable hangs in the form of a parabola, find its equation, taking the origin at the lowest point.
Help please...
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A cable suspended form supports that are the same height and 600ft apart has a sag of 200ft.
If the cable hangs in the form of a parabola, find its equation, taking the origin at the lowest point.
:
They don't give us the height of the supports, so we assume it sags to the ground and their height is 200 ft
:
x = horizontal distance from origin
y = height
:
Two pairs
x=-300, y=200 and x=+300, y=200
Find a
-300^2a - 300b = 200
+300^2a + 300b = 200
Which is
90000a - 300b = 200
90000a + 300b = 200
--------------------addition eliminates b, find a
180000a = 400
1800a = 4
a = 4/1800
a = .002222
b = 0 for an equation, where minimum is the origin
Just
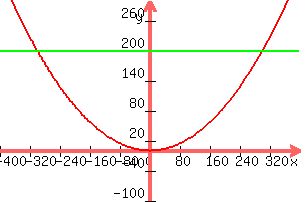
y = .00222x^2 is the equation
looks like this, green horizontal line is 200 ft
|
|
|
| |