At some stops, a certain bus picks up 5 people. At other stops, it picks up 2 and, at the same time lets off 5.
Let x = the number of times the bus increases the no. of passengers by 5.
When the bus picks up 2 and lets off 5, it decreases the no. of passengers
by 3.
Let y = the number of times the bus decreases the no. of passengers by 3.
Then the number of passengers is 5x - 3y
There are no other stops but these. It starts its run empty and picks up 5 people. At the end, it has 11 people aboard.
So we have
5x - 3y = 11
The smallest coefficient in absolute value is |-3| = 3.
So we write 5 and ll in terms of their nearest multiple of 3.
The nearest multiple of 3 to 5 is 6, so we write 5 as 6-1,
The nearest multiple of 3 to 11 is 12, so we write 11 as 12-1,
(6-1)x - 3y = 12-1
6x - x - 3y = 12 - 1
Divide every term through by 3
2x -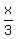 
- y = 4 - 
Isolate all the fractions on the right
2x - y - 4 = -
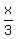The left side is an integer, so the right side is also an
integer. Let that integer be A. Then
2x - y - 4 = A and 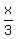- = A
x - 1 = 3A
x = 3A + 1
Substitute 3A+1 for x in the left equation
2(3A+1) - y - 4 = A
6A + 2 - y - 4 = A
6A - 2 - y = A
5A - 2 = y
So we have (x,y) = (3A+1,5A-2)
----------------------------------------
a. If the number of stops is greater than 75, what is the least number of stops the bus makes?
x + y > 75
Substitute (x,y) = (3A+1,5A-2)
3A+1 + 5A-2 > 75
8A-1 > 75
8A > 76
A >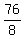 
A > 9.5
x + y increases with increasing A, so the
minimum value of x+y (the number of stops, is when A
is the smallest integer greater than 9.5, which is 10.
Therefore (x,y) = (3A+1,5A-2) = (3·10+1,5·10-2) = (31,48)
So the smallest number of stops is the minimum value of x+y = 31+48 = 79
--------------------------------------------------------
b. If the number of stops is greater than 703, what is the least number of stops the bus makes?
x + y > 703
Substitute (x,y) = (3A+1,5A-2)
3A+1 + 5A-2 > 703
8A-1 > 703
8A > 704
A > 
A > 88
x + y increases with increasing A, so the
minimum value of x+y (the number of stops), is when A
is the smallest integer greater than 88, which is 89.
Therefore (x,y) = (3A+1,5A-2) = (3·89+1,5·89-2) = (268,443)
So the smallest number of stops is the minimum value of x+y = 268+443 = 711
c. For part A, how many of the stops must be where the total gain in passengers is 5?
That's just the value of x for part a, which is 31.
For part B?
That's just the value of x for part b, which is 268.
Edwin
