Question 697326: Find all real zeros of the function: g(x)=(x^3)-2x+1
Answer by Positive_EV(69)   (Show Source):
You can put this solution on YOUR website! A good place to start looking for solutions to cubic functions is to use the Rational Root theorem to try to find rational roots, then use any root found to find a depressed quadratic equation. Any rational roots of a polynomial must be in the form +/- p/q, where p is any number that divides evenly into the constant term, and q is any number that divides evenly into the coefficient of the term with the highest degree. In this case, the constant term is 1 and the coefficient of the x^3 term is also 1, so the only possible rational roots are 1 and -1. Plugging these into the expression yields:
 , so 1 is a zero.
 , so -1 is not a zero.
Since one zero is now known, you can use synthetic division to find a depressed quadratic equation:
| 1 |
|
1 |
0 |
-2 |
1 |
|
|
|
1 |
1 |
-1 |
|
|
1 |
1 |
-1 |
0 |
From this, looking at the bottom row of the synthetic division, the depressed equation is  . Use the quadratic formula to solve for x, where a = 1, b = 1, c = -1:
So the three zeros are 1 and  .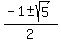
|
|
|
