Question 697075: The population of a town was 10 million on January 1, 2009. The exponential growth function  represents the population of the town. If A represents the population of this town t, years after 2009 and P is the original population. In what year will the population first surpass 15 million?
My teacher has us first figure out what each letter stands for:
15 million A:population of the town
X t: time (years)
10 million p: original population
I'm not sure where the numbers go. meaning, does A=15 million, t is what we are solving for, and P is 10 million? They give 10 million as the towns population and ask what year it will surpass to 15 million. would this be the equation:
15,000,000=10,000,000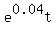
if so this is how to solve the word problem, this is how I continued to solve it:
15,000,000=10,000,000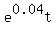
5,000,000=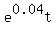
then I used Ln and got 5,000,000=0.04t. Then I divided out 0.04 and got 125,000,000.
I know this is wrong. I'm pretty sure it is going to be a logarithm question, I'm just not sure how to set up the exponential growth equation with the given numbers.
Thank you for your help and for your time.
Answer by nerdybill(7384)   (Show Source):
|
|
|
