SOLUTION: A secretary types five letters and five envelopes but puts the letter into the envelopes at random. What is the probability that at least one letter is put into its correct envelo

When you see the words "at least one", we know to first find the probability of
the complement event and then subtract from 1.

The complement event is that no letters go in the right envelope.

The denominator of the probability is obviously 5!.

The numerator of the probability is what is difficult.

Let an be the number of ways n letters can all put in n wrong envelopes.

We want to find a5  

Suppose the 5 letters are numbered 1,2,3,4,5, and the envelopes are also
numbered 1,2,3,4,5. We have to find the number of ways in which no letter goes
in the envelope having the same number as its number. There are 4 ways for the
first letter to go in an envelope other than the 1st one.  Let us assume, for
definiteness, that the letter 1 gets put in envelope 3.  There are now two
possibilities:

case 1. letter 3 goes in envelope 1,

That leaves letters 2,4,5 to be put wrongly in envelopes 2,4,5.  That's
a3 possibilities.

case 2. letter 3 does not go in envelope 1.

That leaves letters 2,3,4,5 to put wrongly in envelopes 1,2,4,5. But since
letter 3 cannot go in envelope 1, that will be the same as if we re-labeled
letter 3 as letter X and re-labeled envelope 1 as envelope X. Then we would
have letters 2,X,4,5 to go wrongly in envelopes X,2,4,5.  That's a4
possibilities.
   
So the number of ways letter 1 could have gone in envelope 3 is 
a3 + a4 

But we could have put letter 1 in any of the 4 letters {2,3,4,5}.  Therefore we
must multiply that by 4, and so we get

a5 = 4(a3 + a4)

By the same token

a4 = 3(a2 + a3) 

It's obvious that a2 = 1 because if there are 2 letters and 2
envelopes, then there is exactly 1 way to put letter 1 in envelope 2 and letter
2 in envelope 1.

It's also easy to discover that a3 = 2 because envelopes 1,2,3 could
only either go respectively in envelopes 2,3,1 or respectively in envelopes
3,1,2.

Therefore, 

a4 = 3(a2 + a3) = 3(1+2) = 3(3) = 9

and

a5 = 4(a3 + a4) = 4(2+9) = 4(11) = 44

So the probability that all the letters will go wrong is 44 ways out of all 5!
ways they could have been placed. That probability is  =  = .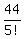

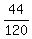Therefore the probability that at least one letter goes in the correct envelope
is 1 -  = 

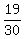Edwin