Question 696743: x^2/25-y^2/9=1
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
you have 
The hyperbola is centered on a point ( , ,  ), which is the "center" of the hyperbola. In your case ), which is the "center" of the hyperbola. In your case  and and  ; so the center is at ( ; so the center is at ( , ,  ) )
 ...=>... ...=>... ....the vertices are ....the vertices are  units to either side units to either side
 ...=>... ...=>...
vertices: (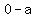 , , ) and ( ) and (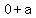 , ,  )......=>....( )......=>....( , ,  ) and =>....( ) and =>....( , ,  ) and ( ) and ( , ,  ) )
The equation  tells us that tells us that  , so , so  which is which is  , ..=>...and the , ..=>...and the 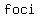 being being  units to either side of the center. units to either side of the center.

|
|
|