Question 696450: Solve for all real numbers. Base your answers on the unit circle and fundamental period accordingly.
2sin(2θ)=3
The answer is: (pi/6, n pi, pi/3 + n pi)
I don't know what it's asking me to do, so I have no idea how to go about even starting the problem. Please try to help! Thank you!
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Something got lost in transcription here,
 <--> <-->  cannot be, cannot be,
because  and and 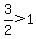
The problem should say 
 --> --> 
Here is the unit circle with the angles that have a sine of 
 The unit circle is a circle of radius 1, centered at the origin of a x-y coordinate system. The unit circle is a circle of radius 1, centered at the origin of a x-y coordinate system.
Angles on the unit circle are turns or sweeps starting at ray OA.
Counterclockwise turns are positive, clockwise turns are negative angles.
You can go more than one turn, as in "turn the knob  ", meaning one and a half turns counterclockwise. ", meaning one and a half turns counterclockwise.
Angle AOB measures  , ,  of a turn, of a turn,
but we prefer to measure it in terms of the arc length from A to B,
which is  of the of the  length of the circumference, length of the circumference,
so it is  . .
We say we measure it in "radians" meaning it's the length of the arc measured with the radius as a unit.
We construct right triangle POB, and define the function sine of AOB as the y-coordinate of B, which is the length of segment PB.
Triangle POB is half of triangle (not drawn, you'll have to imagine it) AOB, which is an equilateral triangle.
PO is half of AO, so its length is  . .
The length of PB is  , of course. , of course.
Applying Pythagoras, we can find that the length of PB is  , so , so
 . .
The segment OC is the mirror image of OB, and has the same y-coordinate.
Angle AOC measures  or or  radians, radians,
and  . .
Other angles that have the same sine differ in a whole number of turns,
ending in ray OB or ray OC after turning clockwise
(same as going to that ray counterclockwise, but then taking a full turn clockwise),
or turning more than one turn in either direction before ending in that ray.
The function sine repeats itself periodically after one turn ( radians) radians)
so we say that the fundamental period of the sine function is  . .
can write their measure as
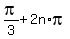 or or 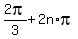 , where , where  is an integer. is an integer.
In conclusion, from  we conclude that we conclude that
 --> -->  --> --> 
or 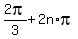 --> -->  --> --> 
|
|
|