Question 694573: What is the basis for the distributive property? I know that the equation is a(b+c)= ab+ac , but I am confused when it gets to a question like this:
Expand using the distributive property:
2m(xy-3p)
Found 3 solutions by ReadingBoosters, Ave, RedemptiveMath:
Answer by ReadingBoosters(3246)   (Show Source): (Show Source):
You can put this solution on YOUR website! Mulitply each term inside the parentheses by what is outside the parentheses.
...
Therefore,
2m(xy-3p) is 2m*xy - 2m*3p yielding 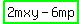
……………….
Have more questions? Get them all answered at once.
HomeworkHelpers@readingboosters.com
Understand your homework, prepare for upcoming tests, improve your scores.
www.MyHomeworkAnswers.com
Answer by Ave(106)   (Show Source): (Show Source):
You can put this solution on YOUR website! Distributive property is just saying, in a super complicated way, to multiply that out.
2m(xy-3p) multiply 2m by both the terms inside -> 2m(xy) and 2m(3p)
2mxy-6mp <-answer
Answer by RedemptiveMath(80)   (Show Source): (Show Source):
You can put this solution on YOUR website! I think you understand the basis of the distributive property. This problem looks more complicated because it has all of these variables. Below are some problems that involve the distributive property. I will start out using simple multiplication with parentheses.
2(3) = 3*2 = 6
2(x+4) = x*2 + 4*2 = 2x + 8
2(x-m) = x*2 - m*2 = 2x - 2m
2x(3) = 3*2x = 6x.
These problems are simpler distribution in the sense that they do not have as much variables and numbers as the problem we need to simplify. However, the method does not change from these to the one we have to deal with. We have the general form
a(b+c) = ab+ac.
In this form, we only see one item per piece in the left side of the equation. That is, the variables are not side by side like xy or ab (looking at the left side). We have "a" that is on the outside of the parentheses. We have "b" and "c" on the inside, but they are not together like bc. These are all single items that are by themselves. On the right side, however, we see that we have two items per piece. That is, we have "ab" and "ac" on the right side. We understand that we get ab and bc because we multiplied a and b and we multiplied a and c on the left side. When we multiply variables, we combine them side by side like this equation shows. When we multiply numbers and variables, we place them side by side like in some of the examples that were shown above.
Now if you take our problem, you notice that there are more variables and numbers. That is perhaps the only difference between this problem and the previous distribution problems. The form a(b+c) = ab+ac shows one item per item on the left. Our problem shows 2 items per piece on the left side (2m, xy and -3p). When we multiply using distribution, we do the same thing as if there were only one item per piece on the left:
2m(xy-3p) = xy * 2m - 3p * 2m...
We multiply 2m by the first piece, xy, and we multiply 2m by the second piece, -3p. We use every number and variable in the multiplication process, but we keep them together in their piece. For example, when we multiply 2m over, we keep it as 2m. We don't multiply everything in the parentheses by 2 and then by m. We multiply everything in the parentheses by 2m. We finish our problem as so:
2m(xy-3p) = xy * 2m - 3p * 2m = 2mxy - 6mp.
Again, just like we would multiply any other distribution problem, we just combine every item per piece in the problem. Xy * 2m becomes 2mxy (2m and xy placed side by side). When we multiply two pieces that have numbers in them, we multiply the numbers together. So, -3p * 2m gives us -6mp (2*-3 = -6). We place the variables side by side next to the new number.
I hope I wasn't too confusing with the "item" and "piece" terminology. If you can think of the terms (2m, xy, and -3p) as pieces and their parts as items, it may be easier when we combine them in multiplication. Remember, we don't break any piece up (we multiply 2m, not 2 first and m second) and we multiply everything in the parentheses by the piece outside of the parentheses. When we multiply two pieces that have numbers (2m and -3p), we actually multiply the numbers (-6mp, not -32mp or 23mp).
|
|
|