|
Question 694400: Hey I was hoping you could help me out. My math problem is the following.
9x^2+25^2=1. I understand that this is the formula for an ellipse, but I am unaware of how to proceed with finding the vertices, the foci, and how to graph it. Am I supposed to divide both side by 9 and 25 to achieve x^2/a+y^2/b=1? My problem is making the right side equal out to 1. Thanks for any help!
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! You probably meant

and want to express it in the form
 , ,
which is appropriate for an ellipse centered at the origin, with axes along the x- and y-axes.
You could write your equation as
 or as or as 
Even without re-writing the equation, it was obvious that it was the equation for an ellipse centered at the origin, with axes along the x- and y-axes, because there were no terms in  or or  , or , or  . .
VERTICES:
The vertices, then, are the intersections with the x- and y-axes, were  and and  , and those are points you need to graph the ellipse. , and those are points you need to graph the ellipse.
 --> -->  --> -->  --> -->  or or  gives you vertices (-1/3,0) and (1/3,0). gives you vertices (-1/3,0) and (1/3,0).
 --> -->  --> -->  --> -->  or or  gives you co-vertices (0,-1/5) and (0,1/5). gives you co-vertices (0,-1/5) and (0,1/5).
AXES:
Vertices (-1/3,0) and (1/3,0) are farther from center (0,0) than co-vertices (0,-1/5) and (0,1/5):
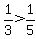 , ,
so the segment between (-1/3,0) and (1/3,0) is called the major axis,
and the segment/distance from each of those vertices to the center is called the semi-major axis, represented as  , ,
so  . .
The distance from the center to the co-vertices is the semi-minor axis:
 . .
FOCI:
The foci would be useful to draw the ellipse if you wanted a very accurate representation.
They are points on both semi-major axes at a distance from the center called the focal distance, represented as  . .
Since for all points of the ellipse the sum of the distances to the foci is constant, the same.
For the vertices, the distance to the nearest focus is 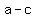 and the distance to the other one is and the distance to the other one is 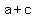 , so the sum is , so the sum is 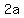 . .
For the co-vertices, the distance to each focus in the hypotenuse of a right triangle with leg lengths  and and  . .
Each of those distances is  , so the sum is , so the sum is  . .
Since that should be the same as for the vertices,
 <--> <-->  --> --> 
That formula allows you to find the focal distance and graph the foci.
 --> -->  --> -->  --> -->  --> -->  --> --> 
So the foci will be at (-4/15,0) and (4/15,0).
GRAPHING:
We can plot the vertices co-vertices and foci, like this
 Then draw the ellipse Then draw the ellipse 
I would just draw a curve that passes through vertices and co-vertices and looks like it could be an ellipse.
To have a real ellipse, you would have to stick pins at the foci; make a loop of thread with a total length (all around) equal to the the distance between the foci, plus the distance between the vertices; throw the loop over the pins; stretch the loop with the tip of a pencil, and draw around keeping the loop fully stretched.
|
|
|
| |