Question 694376: x^4-2x^3+3x^2-2x+1
How to solve without using trial and error method ??
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
Maybe you just wanted to factor the polynomial  . .
Or maybe you wanted to find its zeros, to solve 
I'll try both.
FINDING ZEROS:
We can use a trick that I (dimly) remember from high school.
Obviously  , so , so  is not a zero of the polynomial. is not a zero of the polynomial.
We can divide by  (or by (or by  ) without fear. ) without fear.
When looking for zeros,
 <--> <-->  <--> <--> 
We can do a change of variable.
If we define  , then , then  <--> <--> 
We can re-write  in terms of in terms of  as as
 <--> <-->  <--> <-->  <--> <--> 
Going back to  , remembering we defined , remembering we defined  , ,
 , and multiplying by , and multiplying by  we get we get
 <--> <--> 
Applying the quadratic formula we solve to get

FACTORING (no tricks):
We realize that it is so very symmetrical that if some non-zero  is a zero of is a zero of 
 --> -->  --> -->  --> --> 
So the 4 complex zeros of the polynomial will come in pairs  with with 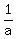 and and  with with  , ,
and the full factoring of the polynomial would be

Multiplying pairs we get

Maybe we could find  and and  and have a partial factoring with real coefficients. and have a partial factoring with real coefficients.
It would be

If it must be  for all for all  , ,
then  and and  <--> <--> 
The solution to  is is  , ,
so substituting into 
the factoring with real coefficients is
 or or 
The factoring with real coefficients is done.
To factor further we need to go beyond real numbers.
Since 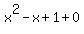 does not have real solutions, does not have real solutions,
any linear 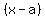 factor would have an imaginary factor would have an imaginary  coefficient. coefficient.
|
|
|