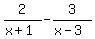SOLUTION: Subtract and simplify: {{{2/(x+1)-3/(x-3)}}} please show all steps

The LCD is the product of the denominators :

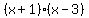We ask ourselves:

What factor does the denominator of the first fraction
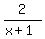, which is 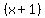, lack which the LCD contains?

The answer is that it lacks the factor . 

Therefore we multiply the first fraction by 
which:

(1) Does not change its value because  equals
    1 and multiplying by 1 does not change any value.
(2) It will cause the denominator of the first fraction to be
    the LCD 

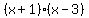So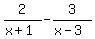 

becomes:



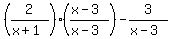Now we do the same with the second fraction. We ask ourselves:

What factor does the denominator of the second fraction
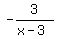, which is , lack which the LCD contains?

The answer is that it lacks the factor .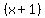 

Therefore we multiply the second fraction by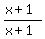 
which:

(1) Does not change its value because 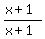 equals
    1 and multiplying by 1 does not change any value.
(2) It will cause the denominator of the second fraction to be
    the LCD 

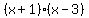So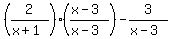  

becomes

    

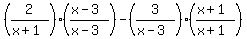or

    

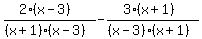Now the denominators are the same, i.e., both denominators
are now equal to the LCD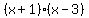 

Multiply the tops out but do not multiply out the bottoms:

    

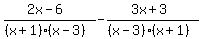Since the denominators are the same we indicate the
subtraction of the numerators over the LCD:



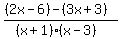Remove the parentheses in the top but not in the bottom:



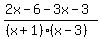Combine terms in the numerator:



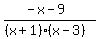I am sure your teacher would accept that answer. But
if you like you can factor -1 out of the numerator:



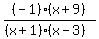and then eliminate the  by putting a negative 
sign out in front of the fraction: