Question 693647: 2x^3-13x^2+24x-9=0
How do I find zeros?
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! Any rational zeros would be of the form  ,
with  being a factor of the constant ( ),
and  being a factor of the leading coefficient ( )
Factors of  are 1, 3, and 9.
Factors of are 1, and 2.
Possible rational zeros are -1/2, -3/2, -9/2, -1, -3, -9, 1/2, 3/2, 9/2, 1, 3, and 9.
Descartes rule of signs helps narrow down your choices.
 has 3 changes of sign going from one coefficient to the next. That means that it has 3 or 1 positive zeros. (It could be two different zeros if one is a double zero).
 has 0 changes of sign, meaning that there are 0 negative zeros.
Now we say that possible rational zeros are 1/2, 3/2, 9/2, 1, 3, and 9.
Trying the possible zeros, using synthetic division, we find out that
Then we recognize that  and have the complete factorization,
 ,
which tells us that the zeros are  (with multiplicity 2, a double zero), and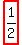 
|
|
|
