SOLUTION: (3x - 10) / (x - 4) >2

Algebra ->  Number-Line -> SOLUTION: (3x - 10) / (x - 4) >2      Log On


   

Question 693272: (3x - 10) / (x - 4) >2
Found 2 solutions by CubeyThePenguin, ikleyn:
Answer by CubeyThePenguin(3113) About Me  (Show Source):
You can put this solution on YOUR website!
(3x-10)/(x-4) > 2
(3x - 10) > 2(x - 4)
3x - 10 > 2x - 8

x > 2

Answer by ikleyn(52775) About Me  (Show Source):
You can put this solution on YOUR website!
(3x - 10) / (x - 4) > 2
~~~~~~~~~~~~~~~~


            The solution in the post by  @CubeyThePenguin is  ABSOLUTELY  WRONG.

            I came to bring the correct solution. 


Transform the inequality, using equivalent transformations

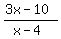    %283x-10%29%2F%28x-4%29 > 2

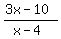    %283x-10%29%2F%28x-4%29 - 2 > 0

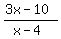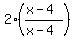    %283x-10%29%2F%28x-4%29 - 2%2A%28%28x-4%29%2F%28x-4%29%29 > 0

    %28%283x-10%29+-+2%2A%28x-4%29%29%2F%28x-4%29 > 0

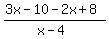    %283x+-+10+-+2x+%2B+8%29%2F%28x-4%29 > 0

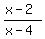    %28x+-2%29%2F%28x-4%29 > 0    (*)


Inequality (*) is equivalent to the given inequality.


There are two critical points x= 2 and x= 4, that divide the number line in three non-intersecting intervals

          (-oo,2), (2,4) and (4,oo).


In the first interval, both the numerator and denominator of (*) are negative;  so the inequality (*) is valid; 
so the interval (-oo,2)  is the part of the solution set.


In the second interval, the numerator of (*) is positive, while the denominator of (*) is negative;  
so the inequality (*) is not valid; thus the interval (2,4)  is NOT the part of the solution set.


In the third interval, both the numerator and denominator of (*) are positive;  so the inequality (*) is valid; 
so the interval (4,oo)  is the part of the solution set.


ANSWER.  The solution set to the given inequality is the union of two intervals  (-oo,2) U (4,oo).

Solved.