SOLUTION: in triangle ABC, C is a right angle. Point M is the midpoint of AB, Point N is midpoint of AC and O is the midpoint of AM. Perimeter of traingle is 112 and ON is 12.5. What is the

Median ON of right triangle AMN
is drawn to the hypotenuse AM,
which divides right triangle AMN
into two isosceles triangles.

Therefore ON=AO=OM=12.5.  (All
three can be seen to be radii of
the green semicircle which inscribes
right angle ANM.)

Therefore AM = 2×12.5 = 25

By the Pythagorean theorem on 
right triangle AMN,

MN² + AN² = AM²
  x² + y² = 25²
  x² + y² = 625 

Each side of triangle AMN is one-
half of the corresponding sides
of triangle ABC, so its perimeter
is one-half of the perimeter of
triangle ABC, therefore

MN + AN + AM = ·112 = 56

  x + y + 25 = 56

       x + y = 31

So we solve the system of equations



by substitution and we get 2 
solutions, 

(x,y) = (24,7) and (x,y) = (7,24).

Using the first solution:

AC = 2·MN = 2x = 2(24) = 48.
NC = y = 7.

So the two parallel side of trapezoid
MNCB are AC=48 and MN=24, and the
height is NC = 7, so the area, using
the area formula for a trapezoid:

Area = 

Area =  = 252.

(x,y) = (7,24).

Using the second solution:

AC = 2·MN = 2x = 2(7) = 14.
NC = y = 24.

So the two parallel side of trapezoid
MNCB are AC=14 and MN=24, and the
height is NC = 24, so the area, using
the area formula for a trapezoid:

Area = 

Area = 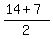 = 252.

So both solutions gives the same area of 252.

The drawing above is drawn approximately to scale
for the first solution,  Here is the way the
drawing would look for the second solution.



So there are two drawings being talked about here,
but both have the same area of MNCB, which is 252.

Edwin