Question 69099: 4) CLASSIC PROBLEM - A traveling salesman (selling shoes) stops at a farm in the Midwest. Before he could knock on the door, he noticed an old truck on fire. He rushed over and pulled a young lady out of the flaming truck. Farmer Crane came out and gratefully thanked the traveling salesman for saving his daughter’s life. Mr. Crane insisted on giving the man an award for his heroism.
So, the salesman said, “If you insist, I do not want much. Get your checkerboard and place one grain of wheat on the first square. Then place two grains of wheat on the next square. Then place four grains on the third square. Continue this until all 64 squares are covered with grains of wheat.” As he had just harvested his wheat, Mr. Crane did not consider this much of an award, but he soon realized he made a miscalculation on the amount of wheat involved.
a) How much wheat would Mr. Crane have to put on the 24th square?
Answer:
Show work in this space.
b) How much total grain would the traveling salesman receive if the checkerboard only had 24 squares?
Answer:
Show work in this space.
c) Calculate the amount of wheat necessary to fill the whole checkerboard (64 squares). How much wheat would the farmer need to give the salesman? Please provide the answer in either scientific notation, or calculate and show all 20 digits.
Answer:
Answer by Earlsdon(6294)   (Show Source): (Show Source):
You can put this solution on YOUR website! Well, you can start by noting that the number of grains of wheat, starting with one on the firsy square, double for each succeeding square. This can be represented by powers of 2 as shown below. If we let n be the number of the square (for the first square, n=1, for the second square, n=2, etc) you can make a table showing the progression of the number of grains on the squares.
n...# of grains
--------------
1.....1
2.....2
3.....4
4.....8
5.....16
It doesn't take long to see that this can be represented by the following"
n. .... grains
--------------
n=1...
n=2...
n=3...
n=4...
n=5...
.
.
.
For the nth square only, the number of grains is 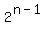
The number of grains on the 24th square only, would be  = 8,388,608 = 8,388,608
The total number of grains on the board is given by:
(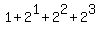 ... ... ) - 1 ) - 1
Now if the checker board had only 24 squares and each square is filled according to the above scheme, then the total number of grains is:

To fill the entire board of 64 squares, you would need:
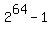 = 18,446,744,073,709,551,615 grains of wheat. = 18,446,744,073,709,551,615 grains of wheat.
|
|
|