Question 69024: 2) Use the geometric sequence of numbers 1, 3, 9, 27, … to find the following:
a) What is r, the ratio between 2 consecutive terms?
Answer:
Show work in this space.
b) Using the formula for the nth term of a geometric sequence, what is the 10th term?
Answer:
Show work in this space.
c) Using the formula for the sum of a geometric series, what is the sum of the first 10 terms?
Answer:
Show work in this space.
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! a)
Since this series is geometric, there is a factor that you must multiply to get from term to term. To find this factor simply divide any nth term, n can be 2 in this case, and the previous term before it, n-1. So picking 3 as n and 1 as n-1 the ratio r is 
So  and it allows me to go from 3 to 9, 9 to 27, etc. and it allows me to go from 3 to 9, 9 to 27, etc.
b)
Now that I know the ratio between two terms I can easily find any term that I want. Since I know that ratio is 3, this series is simply 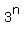 , because any term involves multiplying 3's. So to find the tenth term, just plug in n=9 (the first term is zero) into , because any term involves multiplying 3's. So to find the tenth term, just plug in n=9 (the first term is zero) into 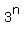 to get to get  so the tenth term is 19683 so the tenth term is 19683
c)
Instead of taking forever and deriving the formula, I'm just going to give it to you. I know it's a bad habit, but this seems a little advanced for algebra or geometry, so I have no idea of what level you're at. Also it not only takes a while to derive, but takes a lot of understanding as well, which should be reserved for a dedicated lesson. Anyway the sum of a geometric series to the nth term is:
 in this case a=1 in this case a=1
So 


If you want to verify this simply calculate all ten terms and add them all up, fun huh?
|
|
|