T(w)= 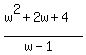 Change Y(w) to y and w to x
y =
Change Y(w) to y and w to x
y = 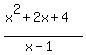 That has a vertical asymptote. Set denominator = 0
x-1 = 0
x = 1
So here is the vertical asymptote:
That has a vertical asymptote. Set denominator = 0
x-1 = 0
x = 1
So here is the vertical asymptote:
 It has no horizontal asymptote because the numerator's largest
power of x (its degree) which is 2 is larger that the denominator's largest
power of x (its degree) with is 1.
However since the degree of the numerator is exactly one more
than the degree of the denominator, it has a slanted or "oblique" asymptote.
We find that by long division:
x+3
x-1)x²+2x+4
x²- x
3x+4
3x-3
7
So y = x+3 +
It has no horizontal asymptote because the numerator's largest
power of x (its degree) which is 2 is larger that the denominator's largest
power of x (its degree) with is 1.
However since the degree of the numerator is exactly one more
than the degree of the denominator, it has a slanted or "oblique" asymptote.
We find that by long division:
x+3
x-1)x²+2x+4
x²- x
3x+4
3x-3
7
So y = x+3 + 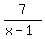 And the fraction
And the fraction 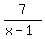 gets smaller and smaller as x gets
larger and larger either positively or negatively, so the curve
approaches just being like the line y = x+3 ignoring the remainder
or denominator. So we draw the slant asymptote y = x+3
gets smaller and smaller as x gets
larger and larger either positively or negatively, so the curve
approaches just being like the line y = x+3 ignoring the remainder
or denominator. So we draw the slant asymptote y = x+3
 The y-intercept is gotten by substituting x=0
y =
The y-intercept is gotten by substituting x=0
y = 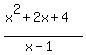 y =
y = 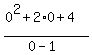 y =
y =  y = -4
So the y-intercept is (0,-4). There is no x-intercept because the numerator
is never zero. So we plot the y-intercept and get a few more points, maybe
(8,12),(-6,-4), (2,12), (-4,-2.4), (3,9.5), (-1,-1.5). and draw the graph:
y = -4
So the y-intercept is (0,-4). There is no x-intercept because the numerator
is never zero. So we plot the y-intercept and get a few more points, maybe
(8,12),(-6,-4), (2,12), (-4,-2.4), (3,9.5), (-1,-1.5). and draw the graph:
 Edwin
Edwin