Question 68761: 1. How many liters of a 50% solution should be added to a 80% solution to obtain a 60% solution?
2. Raymond takes a road trip from Sacramento, CA to South Lake Tahoe, CA. He follows the highway, driving a distance of 100 miles each way. On the drive to South Lake Tahoe he averages 40 mph and on the return trip averages 50 mph. What was his average speed for the entire trip?
3. A course consits of four 100 point exams. A student scores 60 points on the first exam. What average must be obtained on the next three exams to obtain an overall average of 75%?
4. There are only two operations that can be done to expressions that will not change their value. What are they?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1. How many liters of a 50% solution should be added to a 80% solution to obtain a 60% solution?
:
You should specify the amount of 60% solution is desired, in order to show the
method here, I will specify that 12 liters of 60% solution is required
:
Let x = amt of 50% solution required
:
The (12-x) = amt of 80% solutions required
:
.5x + .8(12-x) = .6(12)
.5x + 9.6 - .8x = 7.2
.5x - .8x = 7.2 - 9.6
-.3x = -2.4
x = -2.4/-.3
x = +8 liters of the 50% solution
:
Check our solution: 12 - 8 = 4 liters of the 80% solutions:
Check on a calc: .5(8) + .8(4) = .6(12)
:
:
2. Raymond takes a road trip from Sacramento, CA to South Lake Tahoe, CA. He follows the highway, driving a distance of 100 miles each way. On the drive to South Lake Tahoe he averages 40 mph and on the return trip averages 50 mph. What was his average speed for the entire trip?
:
We want to find the total time of the round trip and divide that into 200:
:
time = dist/speed
(100/40) + (100/50) =
2.5 + 2 = 4.5 hrs for the round trip:
:
Average speed = 200/4.5 = 44.44 mph
:
:
3. A course consists of four 100 point exams. A student scores 60 points on the first exam. What average must be obtained on the next three exams to obtain an overall average of 75%?
:
Let x = the score required on each of the 3 exams to obtain 75%
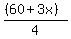 = 75 = 75
:
Mult equation by 4 to get rid of the denominator:
60 + 3x = (75)
60 + 3x = 300
3x = 300 - 69
3x = 240
x = 240/3
x = 80% the average of the remaining 3 exams.
:
Check: 60 + 3(80) divide by 4 = 75
:
:
4. There are only two operations that can be done to expressions that will not change their value. What are they?
:
How about multiplying by 1, and dividing by 1, Adding 0, subtracting 0
|
|
|