SOLUTION: For the function g(x) = 1/x-4 + 2: Write the equations of the asymptotes and label them on the coordinate plane. Enter at least five values in the table of values. Graph the fun

Algebra ->  Rational-functions -> SOLUTION: For the function g(x) = 1/x-4 + 2: Write the equations of the asymptotes and label them on the coordinate plane. Enter at least five values in the table of values. Graph the fun      Log On


   

Question 687244: For the function g(x) = 1/x-4 + 2:
Write the equations of the asymptotes and label them on the coordinate plane.
Enter at least five values in the table of values.
Graph the function on the coordinate plane.
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
I believe you mean g(x) = 1/(x-4) + 2,
which I can write as
g%28x%29=1%2F%28x-4%29%2B2.

The function 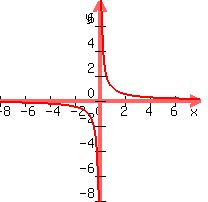f%28x%29=1%2Fx graph%28200%2C200%2C-8%2C8%2C-8%2C8%2C1%2Fx%29 is sort of an ancestor of your function.
It has the x- and y-axes for asymptotes.
The y-axis, x=0 is a vertical asymptote
because the function does not exist for x=0 (it is not continuous at x=0)
but as you approach x=0, from either side,
abs%28f%28x%29%29=abs%281%2Fx%29 grows without bounds.
The horizontal x-axis, y=0, is an asymptote because as abs%28x%29 grows larger (at both ends of the x-axis),
f%28x%29=1%2Fx approaches zero.

The function 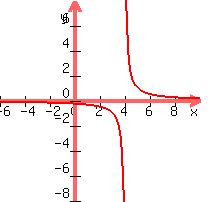h%28x%29=1%2F%28x-4%29 graph%28200%2C200%2C-6%2C10%2C-8%2C8%2C1%2F%28x-4%29%29
is the same, but moved 4 units to the right, a closer ancestor.
Its asymptotes are x=4%7D%7D+and+%7B%7B%7By=0.
x=4 (vertical asymptote, where the function is not continuous), and
y=0 (again).

Adding 2 to that function gives you g%28x%29=1%2F%28x-4%29%2B2.
The graph is graph%28200%2C200%2C-6%2C10%2C-4%2C12%2C1%2F%28x-4%29%2B2%2C2%29
and the asymptotes are y=2 and
x=4.

Just five points seems too little for this function, but the symmetry might help.
For x=4.1, g%28x%29=1%2F%284.1-4%29%2B2=1%2F0.1%2B2=10%2B2=12.
(Symmetrically, for x=3.9, g%28x%29=1%2F%283.9-4%29%2B2=1%2F%28-0.1%29%2B2=-10%2B2=-8.
For x=4.5, g%28x%29=1%2F%284.5-4%29%2B2=1%2F0.5%2B2=2%2B2=4.
(Symmetrically, for x=3.5, g%28x%29=1%2F%283.5-4%29%2B2=1%2F%28-0.5%29%2B2=-2%2B2=0.
For x=5, g%28x%29=1%2F%285-4%29%2B2=1%2F1%2B2=1%2B2=3.
(Symmetrically, for x=3, g%28x%29=1%2F%283-4%29%2B2=1%2F%28-1%29%2B2=-1%2B2=1.
Forx=9, g%28x%29=1%2F%289-4%29%2B2=1%2F5%2B2=0.2%2B2=2.2.
(Symmetrically, for x=-1, g%28x%29=1%2F%28-1-4%29%2B2=1%2F%28-5%29%2B2=-0.2%2B2=1.8.
Forx=14, g%28x%29=1%2F%2814-4%29%2B2=1%2F10%2B2=0.1%2B2=2.1.
(Symmetrically, for x=-6, g%28x%29=1%2F%28-6-4%29%2B2=1%2F%28-10%29%2B2=-0.1%2B2=1.9.
We can plot those points as blue dots and connect them.
We can draw the asymptotes in green too.