SOLUTION: explain why f(x)= 3x raise to the 2nd power-7x/xraise to the third power is not a polynomial function.

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: explain why f(x)= 3x raise to the 2nd power-7x/xraise to the third power is not a polynomial function.      Log On


   

Question 684490: explain why f(x)= 3x raise to the 2nd power-7x/xraise to the third power is not a polynomial function.
Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
A polynomial must be equivalent to an expression with a finite number of
terms all of which are in the form ħAxN where N is a non-negative
whole number, which includes 0, but not negative numbers.  A can be any
number, positive, negative or 0.  

f(x) = 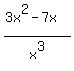%283x%5E2-7x%29%2Fx%5E3 is not a polynomial because it has a variable
in a denominator.  Its numerator is a polynomial and its denominator is
a polynomial, but f(x) itself is not a polynomial.

Even if it is written as

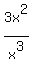
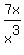f(x) = 3x%5E2%2Fx%5E3%22%22-%22%227x%2Fx%5E3

and then as

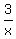
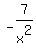f(x) = 3%2Fx%22%22-%22%22-7%2Fx%5E2 where x is not = 0, its terms are not of the form ħAxN, 
where A is any number and N a non-negative whole number.

And even if it is further written as

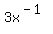
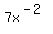f(x) = 3x%5E%28-1%29%22%22-%22%227x%5E%28-2%29 where x is not = 0, its terms are not of the form ħAxN, 
where A is any number and N a non-negative whole number. 
 
So f(x) cannot be changed into a finite number of terms all of the form
AxN, where A is any number and N a non-negative whole number. 
So f(x) is not a polynomial.

Edwin