Question 683812: Two trains of equal length are on parallel tracks. One train is travelling at
40 km/h and the other at 20 km/h. It takes two minutes longer for the trains
to completely pass one another when going in the same direction, than when
going in opposite directions.
Determine the length of each train.
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website! Two trains of equal length are on parallel tracks. One train is travelling at
40 km/h and the other at 20 km/h. It takes two minutes longer for the trains
to completely pass one another when going in the same direction, than when
going in opposite directions.
Determine the length of each train.
Let's convert their speeds to km/minute
20 km/h =  km/minute = km/minute =  km/minute
40 km/h = km/minute
40 km/h =  km/minute = km/minute =  km/minute
Let each train's length be x, and the time to pass when going in
opposite directions be t minutes. Then the time to pass when going in
the same directions will be t+2.
Here they are going in opposite directions starting to pass each other: km/minute
Let each train's length be x, and the time to pass when going in
opposite directions be t minutes. Then the time to pass when going in
the same directions will be t+2.
Here they are going in opposite directions starting to pass each other:
 Suppose the train on the left is the faster train. For the train on the
left to pass the train on the right, point A must move to be even with
point B.
Point A is approaching point B at a rate equal to the sum of the rates
or
Suppose the train on the left is the faster train. For the train on the
left to pass the train on the right, point A must move to be even with
point B.
Point A is approaching point B at a rate equal to the sum of the rates
or 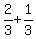 or 1 km/minute. Point A's distance to point B is 2x.
Since distance = rate·time, we have 2x = 1·t
Here they are going in the same direction, the faster starting to pass
the slower. or 1 km/minute. Point A's distance to point B is 2x.
Since distance = rate·time, we have 2x = 1·t
Here they are going in the same direction, the faster starting to pass
the slower.
 Suppose again the train on the left is the faster train. As above, for the
train on the left to pass the train on the right, point A must move to be
even with point B. In this case Point A is approaching point B at a rate equal
to the difference of the rates or
Suppose again the train on the left is the faster train. As above, for the
train on the left to pass the train on the right, point A must move to be
even with point B. In this case Point A is approaching point B at a rate equal
to the difference of the rates or 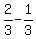 or or  km/minute. Again, point A's distance
to point B is 2x. Since distance = rate·time, in this case we have 2x = km/minute. Again, point A's distance
to point B is 2x. Since distance = rate·time, in this case we have 2x =  ·(t+2).
So we have this system of equations:
2x = 1·t
2x = ·(t+2).
So we have this system of equations:
2x = 1·t
2x =  ·(t+2)
Solve that system by substitution and get
x = 0.5 km, and t = 1 minute
Each train is 0.5 km long and it takes 1 minute for them to pass
each other when going in opposite directions and 1+2 or 3 minutes
for the faster to pass the slower when going in the same direction.
Edwin ·(t+2)
Solve that system by substitution and get
x = 0.5 km, and t = 1 minute
Each train is 0.5 km long and it takes 1 minute for them to pass
each other when going in opposite directions and 1+2 or 3 minutes
for the faster to pass the slower when going in the same direction.
Edwin
|
|
|