SOLUTION: Let f x = tan(x/2) Show that f({{{2pi}}}) = f({{{4pi}}}) but there is no number c in the closed interval [{{{2pi}}},{{{4pi}}}] such that f'(c) = 0. Why does this not contradict

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: Let f x = tan(x/2) Show that f({{{2pi}}}) = f({{{4pi}}}) but there is no number c in the closed interval [{{{2pi}}},{{{4pi}}}] such that f'(c) = 0. Why does this not contradict      Log On


   

Question 683369: Let f x = tan(x/2)
Show that f(2pi) = f(4pi) but there is no number c in the
closed interval [2pi,4pi] such that f'(c) = 0. Why does this not contradict Rolle's Theorem?
Answer by Edwin McCravy(20064) About Me  (Show Source):
You can put this solution on YOUR website!
Let f(x) = tan(x%2F2)
Show that f(2pi) = f(4pi) but there is no number c in the
closed interval [2pi,4pi] such that f'(c) = 0.
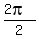f(2pi) = tan(%282pi%29%2F2) = tan(pi = 0
f(4pi) = tan(%284pi%29%2F2) = tan(2pi = 0

f'(x) = 1%2F2secē(x%2F2)

The secant function is never 0, so there can be no value
of c such that f'(c) = 0 on that interval.

Why does this not contradict Rolle's Theorem?
Because Rolle's theorem only says there is such a number c on closed interval
[a,b] in which the function is everywhere defined, continuous and differentiable 
on the closed interval [a,b].  Rolle's theorem is not violated since 
f(x) = tan(x%2F2) is not continuous and differentiable everywhere on the
closed interval [2pi,4pi] for f(x) is not defined ar x = 3pi
which is on the closed interval [2pi,4pi].

Edwin