SOLUTION: I have a problem I can not figure out. In 1975, Visalia had a population of 65,000. In 2000 the population was 99,500. Assuming exponential growth, estimate the population in the 2

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: I have a problem I can not figure out. In 1975, Visalia had a population of 65,000. In 2000 the population was 99,500. Assuming exponential growth, estimate the population in the 2      Log On


   

Question 682835: I have a problem I can not figure out. In 1975, Visalia had a population of 65,000. In 2000 the population was 99,500. Assuming exponential growth, estimate the population in the 2015. Use A=A0e^kt
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
A=A%5B0%5De%5Ekt
For t=0, A=A%5B0%5De%5E%28k%2A0%29 --> A=A%5B0%5De%5E0 --> A=A%5B0%5D%2A1 --> A=A%5B0%5D
A%5B0%5D is the population at whatever time we decide to take as t=o.

Taking 1975 as time zero, t=year-1975, is a good choice.
In 1975, t=1975-1975=0,
Visalia had a population of 65,000, A=A%5B0%5D=65000
Now we can write the exponential function as
highlight%28A=65000e%5Ekt%29,
but we still have to find k.

In 2000, t=2000-1975=25,
and the population was 99,500,
so 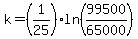A=65000e%5E25k=99500 --> e%5E25k=99500%2F65000 --> 25k=ln%2899500%2F65000%29 --> k=%281%2F25%29ln%2899500%2F65000%29 --> highlight%28k=0.0170308%29 (rounded approximation)
Now we can write the exponential function as
highlight%28A=65000e%5E%280.0170308t%29%29.

In the year 2015, t=2015-1975=40, and we estimate
A=65000e%5E%280.0170308%2A40%29 --> A=65000e%5E0.681232 --> A=65000%2A1.976311 --> highlight%28A=128460%29.