Question 682080: Example 1: Four friends cleaning out their math folders were too lazy to get up and throw the papers in the trash. Instead, they sat at their desks and took shots at the wastebasket. Together they took a total of 188 shots. Only 89 of the shots actually made it in the wastebasket, and of those that went in 32 of them hit the rim before going in. Sixty-four shots missed the rim and did not go in the wastebasket.
a.) How many shots hit the rim but did not go in the wastebasket?
b.) What is the probability a shot hit the rim but did not go in the wastebasket?
P(shot hit the rim and did not go in) =
c.) What is the probability a shot went in the basket?
d.) What is the probability a shot went in if the shot hit the rim?
P(shot made/hit rim) =
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! THE SOLUTION:
a.) How many shots hit the rim but did not go in the wastebasket?
The number of shots that did not go in was  . .
 hit the rim, but did not go in. hit the rim, but did not go in.
b.) What is the probability a shot hit the rim but did not go in the wastebasket?
Adding up, the total number of shots that hit the rim was  . .
P(shot hit the rim and did not go in) = 
c.) What is the probability a shot went in the basket?
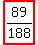 because 89 of 188 went into the basket because 89 of 188 went into the basket
d.) What is the probability a shot went in if the shot hit the rim?
P(shot made/hit rim) = 
because a total of 67 hit the rim, but only 32 of those went in.
TO UNDERSTAND THE PROBLEM:
Each shot could have only one of the 4 outcomes below:
go in the basket without touching the rim,
hit the rim and go in the basket,
hit the rim and fall outside the basket,
miss the basket completely, without even touching the rim.
If we figure out how many shots had each of those outcomes, we can to answer any questions.
In all, 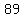 of the of the 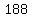 shots went into the basket. shots went into the basket.
The number of shots that did not go in was  . .
Of those 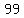 shots, shots,  were really bad shots, that missed the basket without even touching the rim. were really bad shots, that missed the basket without even touching the rim.
The other  hit the rim, but did not go in. hit the rim, but did not go in.
Of the 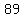 shots that went into the basket, shots that went into the basket,  hit the rim before going in, hit the rim before going in,
The other  shots went in the basket without touching the rim. (That's nice to know, but the problem did not ask any question that required that calculation). shots went in the basket without touching the rim. (That's nice to know, but the problem did not ask any question that required that calculation).
|
|
|