Question 682048: At the same time, but different speed, Mark and Nancy left (driving) from different towns, A and B, and drove toward each other. They first met at the point that was 60 miles from Town A. When Mark and Nancy reached their destinations (B and A, respectively) they drove back without stop. 3 hours later after they originally left the towns (the initial staring points), they met again. This time, the meeting point was 40 miles from town A. Suppose each of them was moving all the time at a constant speed, what were the speeds of Mark and Nancy. (note, they have different speeds).
Thanks for your help! It is much appreciated!!
Found 2 solutions by ankor@dixie-net.com, josmiceli:
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! At the same time, but different speed, Mark and Nancy left (driving) from different towns, A and B, and drove toward each other.
They first met at the point that was 60 miles from Town A.
When Mark and Nancy reached their destinations (B and A, respectively) they drove back without stop.
3 hours later after they originally left the towns (the initial staring points), they met again.
This time, the meeting point was 40 miles from town A. Suppose each of them was moving all the time at a constant speed, what were the speeds of Mark and Nancy.
A diagram will help
A------60------*-----d------B; first meeting
A----40----*----(d+20)------B: 2nd meeting
:
Let d = distance from the 1st meeting point to B, therefore
Initially, M travels 60 mi while N travels d mi
:
To the 2nd meeting:
M travels: d + (d+20) = (2d+20) mi
while
N travels: 60 + 40 = 100 mi
:
The M:N distance relationships are the same for each part of the trip
:
1st meeting = 2nd meeting
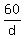 = = 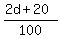
Cross multiply
d(2d+20) = 60 * 100
2d^2 + 20d = 6000
A quadratic equation
2d^2 + 20d - 6000 = 0
simplify, divide by 2
d^2 + 10d - 3000 = 0
This will factor to
(d+60)(d-50) = 0
the positive solution
d = 50 miles from the 1st meeting point to B
then
60 + 2(50) + 20 = 180 miles traveled by M in 3 hrs, therefore
 = 60 mph is M's speed = 60 mph is M's speed
And
50 + 60 + 40 = 150 miles traveled by N in 3 hrs, therefore
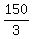 = 50 mph is N's speed = 50 mph is N's speed
Answer by josmiceli(19441)   (Show Source): (Show Source):
|
|
|