|
Question 681942: Find the equation of a hyberbola with transverse axis on the line y= -5, length of transverse axis = 6, conjugate axis on the line x=2. and length of conjugate axis=6. Expres the answer in the form Ax^2 + Cy^2 + Dx + Ey + F = 0.
Found 2 solutions by Edwin McCravy, lwsshak3:
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the equation of a hyberbola with transverse axis on the line y= -5, length of transverse axis = 6, conjugate axis on the line x=2. and length of conjugate axis=6. Expres the answer in the form Ax^2 + Cy^2 + Dx + Ey + F = 0.
The equation of such a hyperbola, with the transverse axis horizontal, is
     where (h,k) is the center, a =
where (h,k) is the center, a =  the length of the transverse axis,
and b = the length of the transverse axis,
and b =  the length of the conjugate axis.
We'll begin by drawing the horizontal line y = -5 and the vertical line x = 2. the length of the conjugate axis.
We'll begin by drawing the horizontal line y = -5 and the vertical line x = 2.
 The transverse axis and the conjugate axis intersect at the center of the
hyperbola which is (2,-5). Now we'll leave just the transverse axis and the
conjugate axis, which are given as 6 units each, and we'll and erase the rest
of those green lines:
The transverse axis and the conjugate axis intersect at the center of the
hyperbola which is (2,-5). Now we'll leave just the transverse axis and the
conjugate axis, which are given as 6 units each, and we'll and erase the rest
of those green lines:
 and draw the defining rectangle: and draw the defining rectangle: Now we can sketch in the asymptotes and the hyperbola:
Now we can sketch in the asymptotes and the hyperbola:
 We can write the equation of the hyperbola,
We can write the equation of the hyperbola,
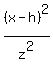     where (h,k) is the center (2,-5), a =
where (h,k) is the center (2,-5), a =  the length of the transverse
axis = the length of the transverse
axis =    = 3
and b = = 3
and b =  the length of the conjugate axis, also = 3 the length of the conjugate axis, also = 3
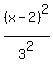  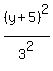  
  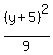   That is the equation in STANDARD, but the problem asks for it in the
GENERAL form Ax² + Cy² + Dx + Ey + F = 0, so
That is the equation in STANDARD, but the problem asks for it in the
GENERAL form Ax² + Cy² + Dx + Ey + F = 0, so
  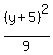   Clear of fractions by multiplying through by 5
(x - 2)² - (y + 5)² = 9
x² - 4x + 4 - (y² + 10y + 25) = 9
x² - 4x + 4 - y² - 10y - 25 = 9
x² - 4x - 21 - y² - 10y = 9
x² - 4x - 30 - y² - 10y = 0
Rearrange the terms in the form Ax² + Cy² + Dx + Ey + F = 0
x² - y² - 4x - 10y - 30 = 0
Edwin
Clear of fractions by multiplying through by 5
(x - 2)² - (y + 5)² = 9
x² - 4x + 4 - (y² + 10y + 25) = 9
x² - 4x + 4 - y² - 10y - 25 = 9
x² - 4x - 21 - y² - 10y = 9
x² - 4x - 30 - y² - 10y = 0
Rearrange the terms in the form Ax² + Cy² + Dx + Ey + F = 0
x² - y² - 4x - 10y - 30 = 0
Edwin
Answer by lwsshak3(11628)   (Show Source): (Show Source):
|
|
|
| |