Question 681830: At the same time but at different speeds, two trains, X and Y, leave from different stations, A and B, and traveled toward each other. They first met at the point that was 120 miles from station A. When X and Y reached their destination (B and A, respectively), they moved back without stop. 6 hours after they first met, the two trains met again. This time, the meeting point was 90 miles from station A. Suppose each of the trains was moving all the time at a constant speed, what were the speeds of Train X and Train Y. (note, X and Y have different speeds).
Thanks for your help!!!
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! At the same time but at different speeds, two trains, X and Y, leave from different stations, A and B, and traveled toward each other.
They first met at the point that was 120 miles from station A.
When X and Y reached their destination (B and A, respectively), they moved back without stop.
6 hours after they first met, the two trains met again.
This time, the meeting point was 90 miles from station A.
Suppose each of the trains was moving all the time at a constant speed, what were the speeds of Train X and Train Y.
:
A diagram will help
A------120------*-----d------B; first meeting
A----90----*----(d+30)------B: 2nd meeting
:
From the given information, after they met the 1st time, y traveled 120 mi to A
Then 90 mi from A to the 2nd meeting, 6 hrs later, therefore:
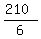 = 35 mph is the y's speed = 35 mph is the y's speed
:
Let d = distance from the 1st meeting point to B, therefore
Initially, x travels 120 mi while y travels d mi
then to the 2nd meeting:
y travels 210 (120+90) mi while x travels (2d+30) mi
:
The distance relationships are the same for each part of the trip
 = = 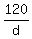
Cross multiply
d(2d+30) = 210 * 120
2d^2 + 30d = 25200
A quadratic equation
2d^2 + 30d - 25200 = 0
simplify, divide by 2
d^2 + 15d - 12600 = 0
This will factor to
(d+120)(d-105) = 0
the positive solution
d = 105 miles from the 1st meeting point to B
then
2(105) + 30 = 240 miles traveled by x in 6 hrs, therefore
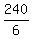 = 40 mph is x's speed = 40 mph is x's speed
:
To summarize: x = 40 mph, y = 35 mph
|
|
|