|
Question 68111: Find the polynomial f(x) of degree three that has zeroes at 1, 2 and 4 such that f(0)=-16.
The degree three polynomial f(x) with real coefficients and leading coefficient 1, has 4 and 3 + i among its roots. Express f(x) as a product of linear and quadratic polynomials with real coefficients.
Given that (3x-a)(x-2)(x-7)=3x^2-32x^2+81x-70, determine the value of a.
Find all roots of the polynomial x^3-x^2+16x-16.
Find the vertical asymptote of the rational function f(x)=3x-12/4x-2.
Find the horizontal asymptote of the rational function f(x)=8x-12/4x-2.
Studying for final exam please respond ASAP. Thanks for your assistance.
Found 2 solutions by Edwin McCravy, stanbon:
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the polynomial f(x) of degree three that has zeroes
at 1, 2 and 4 such that f(0)=-16.
Two ways to do it:
First way:
Rule 1: If a polynomial f(x) has roots r1, r2, r3, ···, rn
and leading coefficient a, then
f(x) = a(x-r1)(x-r2)···(x-rn)
So for this problem:
f(x) = a(x - 1)(x - 2)(x - 4)
-16 = a(0 - 1)(0 - 2)(0 - 4)
-16 = a(-1)(-2)(-4)
-16 = -8a
2 = a
f(x) = 2(x - 1)(x - 2)(x - 4)
f(x) = 2(x - 1)(x² - 6x + 8)
f(x) = 2(x³ - 6x² + 8x - x² + 6x - 8)
f(x) = 2(x³ - 7x² + 14x - 8)
f(x) = 2x³ - 14x² + 28x - 16
Here's the second method:
Let the polynomial be
f(x) = ax³ + bx² + cx + d
Then plugging in the values for x, and
setting it to -16 when 0 is plugged in,
and 0 when the others are plugged in:
f(0) = a(0)³ + b(0)² + c(0) + d = -16
f(1) = a(1)³ + b(1)² + c(1) + d = 0
f(2) = a(2)³ + b(2)² + c(2) + d = 0
f(4) = a(4)³ + b(4)² + c(4) + d = 0
The above simplifies to this system
d = -16
a + b + c + d = 0
8a + 4b + 2c + d = 0
64a + 16b + 4c + d = 0
Substitute =16 for d in the bottom three:
a + b + c - 16 = 0
8a + 4b + 2c - 16 = 0
64a + 16b + 4c - 16 = 0
a + b + c = 16
8a + 4b + 2c = 16
64a + 16b + 4c = 16
Solve that system of equations as you get
a = 2, b = -14, c = 28
So the polynomial
f(x) = ax³ + bx² + cx + d becomes
f(x) = 2x³ - 14x + 28x - 16
---------------------------------------
The degree three polynomial f(x) with real coefficients and
leading coefficient 1, has 4 and 3 + i among its roots.
Express f(x) as a product of linear and quadratic polynomials
with real coefficients.
Rule 2:
If a polynomial has real coefficients, then if a complex
number a + bi is a root, then so is its conjugate a - bi
So the roots are 4, 3+i, 3-i
Using rule 1
f(x) = 1(x - 4)[x - (3+i)][x - (3-i)]
f(x) = (x - 4)[x² - (3-i)x - (3+i)x + (3+i)(3-i)]
f(x) = (x - 4)[x² - 3x + ix - 3x - ix + 9 - i²]
f(x) = (x - 4)[x² - 6x + 9 - i²]
Since i² = -1, substitute -1 for i²
f(x) = (x - 4)[x² - 6x + 9 - (-1)]
f(x) = (x - 4)(x² - 6x + 9 + 1]
f(x) = (x - 4)(x² - 6x + 10)
f(x) = x³ - 6x² + 10x - 4x² + 24x - 40
f(x) = x³ - 10x² + 34x - 40
----------------------------------
Given that (3x-a)(x-2)(x-7)=3x³-32x²+81x-70, determine the
value of a.
Since this is an identity, we may substitute any number for x
and it will be true. It wouldn't do any good to substitute a
root 2 or 7 since that would just give 0 = 0. So let's
substitute x = 0, since that is the easiest number to
substitute, and 0 is not a root:
(3x-a)(x-2)(x-7) = 3x³-32x²+81x-70
[3(0)-a](0-2)(0-7) = 3(0)³-32(0)²+81(0)-70
(-a)(-2)(-7) = -70
-14a = -70
a = 5
Find all roots of the polynomial x^3-x^2+16x-16.
Set it = 0
x³ - x² + 16x - 16 = 0
Factor by grouping:
Factor x² out of the first two terms
and 16 out of the last two terms:
x²(x - 1) + 16(x - 1) = 0
Factor out common factor (x - 1)
(x - 1)(x² + 16) = 0
Set each factor = 0
x - 1 = 0
x = 1
x² + 16 = 0
x² = -16
x = ±Ö-16
x = ±4i
------------------------------------
Find the vertical asymptote of the rational
function f(x)=(3x-12)/(4x-2).
Set denominator = 0
4x - 2 = 0
4x = 2
x = 1/2
------------------------------------------
Find the horizontal asymptote of the rational function
f(x) = 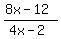 .
Rule: Divide every term on top and bottom by the greatest
power of x
f(x) = .
Rule: Divide every term on top and bottom by the greatest
power of x
f(x) = 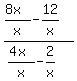 Simplify
f(x) =
Simplify
f(x) = 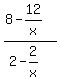 As x grows very large in absolute value, the fractions
get extremely small, and become negligible, so f(x)
approaches the fraction 8/2 or 4, so the horizontal
asymptote is y = 4.
Or you can learn the rule that if the numerator and
denominator have the same degree, the horizontal
asymptote's equation is the quotient of the leading
coefficients, y = 8/4 or y = 2
Edwin
As x grows very large in absolute value, the fractions
get extremely small, and become negligible, so f(x)
approaches the fraction 8/2 or 4, so the horizontal
asymptote is y = 4.
Or you can learn the rule that if the numerator and
denominator have the same degree, the horizontal
asymptote's equation is the quotient of the leading
coefficients, y = 8/4 or y = 2
Edwin
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the polynomial f(x) of degree three that has zeroes at 1, 2 and 4 such that f(0)=-16.
f(x)=a(x-1)(x-2)(x-4)
f(0)=a(-1)(-2)(-4)=-16
-8a=-16
a=2
Therefore: f(x)=2(x-1)(x-2)(x_4)
---------------------------------------------
The degree three polynomial f(x) with real coefficients and leading coefficient 1, has 4 and 3 + i among its roots. Express f(x) as a product of linear and quadratic polynomials with real coefficients.
If the coefficients are Real and 3+i is a root, 3-1 must be a root.
f(x)=(x-4)(x-(3+i))(x-(3-i))
f(x)=(x-4)((x-3)-i)((x-3)+i)
f(x)=(x-4)((x-3)^2-i^2)
f(x)=(x-4)(x^2-6x+9+1)
f(x)=(x-4)(x^2-6x+10)
----------------------------------
Given that (3x-a)(x-2)(x-7)=3x^2-32x^2+81x-70, determine the value of a.
The product of the constants on the left is (-a)(-2)(-7)=-14a
The constant on the right is -70a
Therefore: -14a=-70a
a=5
-----------------------------
Find all roots of the polynomial x^3-x^2+16x-16.
The coefficients add up to zero, so x=1 is a root.
Using synthetic division to divide by x-1 you get:
.....-1)1....-1....16....-16
.........1.....0.....16.|.0
So the quotient is x^2+16
This factors as (x+4i)(x-4i)
By the factor theorem this shows 4i and -4i are roots.
Conclusion: 1, 4i, -4i are the roots
-----------------------------
Find the vertical asymptote of the rational function f(x)=3x-12/4x-2.
You have vertical asymptote candidates when the denominator is zero.
If 4x-2=0, then x=1/2
The numerator is not zero when x=1/2 so you have a vertical asymptote
at x=1/2.
----------------------------
Find the horizontal asymptote of the rational function f(x)=8x-12/4x-2.
The highest power of x in both numerator and denominator is x^1
The coefficients in the numerator and denominator of x^1 give 8/4=2
You have a horizontal asymptote at x=2
----------------
Cheers,
Stan H.
|
|
|
| |