Question 679089: How can I explain an irrational exponent?
Found 2 solutions by lynnlo, MathLover1:
Answer by lynnlo(4176)   (Show Source): (Show Source):
You can put this solution on YOUR website! A IRRATIONAL CAN NOT BE WRITTEN AS A FRACTION
EXAMPLES:
PI
(SQUARE(2)
IF YOU CAN RAISE A NUMBER TO ANY OF THESE
YOU WOULD HAVE A IRRATIONAL EXPONENT
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! recall that, by definition, an exponent can be any number, real or complex, negative or positive, rational or 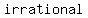 , algebraic or transcendental. , algebraic or transcendental.
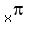 is an example of an irrational exponent is an example of an irrational exponent
or 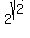 ....how to do this one? ....how to do this one?
we will do it by 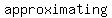 the the  exponent by exponent by  exponents that are closer and closer to the irrational one exponents that are closer and closer to the irrational one
In example 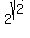 , you want the exponent , you want the exponent  to be to be  equal to equal to 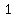 , so the first approximation to , so the first approximation to 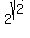 is is  . .
or, go one step further with  , so the second approximation to , so the second approximation to 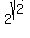 is is  which is approximately which is approximately 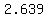
or three significant figures,
 , so you have to take a , so you have to take a 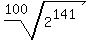 which is approximately which is approximately 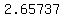 Continuing this way, we get the sequence of approximations: Continuing this way, we get the sequence of approximations:
 , , 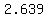 , , 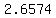 , , 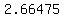 , , 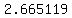 , , 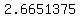 , , 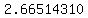 , ... , ...
|
|
|