SOLUTION: graph: f(x)=(x-2)^2 Determine the values of x where the function is increasing, decreasing, and constant.

Algebra ->  Rational-functions -> SOLUTION: graph: f(x)=(x-2)^2 Determine the values of x where the function is increasing, decreasing, and constant.       Log On


   

Question 678982: graph: f(x)=(x-2)^2
Determine the values of x where the function is increasing, decreasing, and constant.
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!
f%28x%29=%28x-2%29%5E2

f%28x%29=x%5E2-4x%2B4

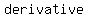Take the derivative f' of the function and set it equal to 0.
You need that because the derivative at a constant point is 0 plus, at that point, the function can change from increasing to decreasing and vice versa.
f'%28x%29+=+2x-4
2x-4=0
2x=+4
x=2, this means that when x+=+2, the slope at x+=2 is 0.
You plug in a number from either side of that number, x= 2 into f'(x) because by doing this you find out the slope of the line.
So I will pick, x+=-3 and x+=3 for simplicity's sake.
2%28-3%29-4+=+-6-4=-10+.....=>..slope is negative
2%283%29-4=+6-4=2 .....=>..slope is positive

so, the function is decreasing for any value of x from (-infinity,2),
increasing for any value of x from (2,infinity)


+graph%28+600%2C+600%2C+-6%2C+10%2C+-10%2C+10%2Cx%5E2-4x%2B4%29+