SOLUTION: How to find the rectangular coordinates, when given the polar coordinates? The coordinate given is (-4,4)

The formula to convert 

Polar point (r,) to the rectangular point (x,y) is given by

x = r·cos(), y = r·cos().

Here r = -4 and  = 4 radians. Substituting, we have:

x = -4·cos(4) = 2.614574483, y = -4·cos(4) = 3.027209981

So the answer is:

the rectangular point (x,y) = (2.614574483, 3.027209981),

or rounded to hundredths, (2.61,3.03).

Let's show how that works: 



When r is positive the point will be in the same quadrant as θ.
On the other hand when r is negative the point will end up in the 
quadrant exactly opposite θ.    


The angle , the second polar coordinate, is 4 radians.  
Converting that to degrees gives us 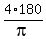 = 229.1831181°,
which is between 180° and 270°. which means it is an angle in the 
3rd quadrant.

Let's first plot the polar point (4,4).  Then we'll reflect it through
the origin to the quadrant opposite 4 radians, which will be the 1st
quadrant.        

We swing a radius 4 units long through an arc counter-clockwise from
the right side of the x-axis 229.1831181° around to the 3rd quadrant,
like this:



The point (4,4) is marked with a small circle.  However we want the 
point (-4,4), not (4,4), so we reflect it through the origin to the
quadrant opposite the 3rd quadrant, which is the 1st quadrant, like
this:



That polar point (-4,4) is the same point as this rectangular point
(2.61, 3.03):



Edwin