SOLUTION: Exponential growth problem using the formula: N= No(R)^t/d N is the current amount, No is the initial amount, R is the rate, t is the time, d is the number of days/months/years

Algebra ->  Test -> SOLUTION: Exponential growth problem using the formula: N= No(R)^t/d N is the current amount, No is the initial amount, R is the rate, t is the time, d is the number of days/months/years       Log On


   

Question 678697: Exponential growth problem using the formula: N= No(R)^t/d
N is the current amount, No is the initial amount, R is the rate, t is the time, d is the number of days/months/years
The population of a city was estimated to be 125000 in 1930 and 500000 in 1998.
a) Estimate the population of the city in 2020.
b) if the population continues to grow at the same rate, when will the population reach 1 million?
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
If we know that N grows exponentially,
we know the "initial" 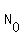N%5B0%5D value of N at some point we take as starting point,
and we know that N grew by a factor of R over a period of d days/months/years (or whatever unit of time),
highlight%28N=N%5B0%5D%2AR%5E%28%28t%2Fd%29%29%29%5Efunction
that gives the value of N at a time t days/months/years (or whatever unit of time we were using) after our starting point.

THE PROBLEM SET-UP:
Here we define
start = year 1930
we measure time in years
t=0 for 1930
t=1998-1930=68 for 1998
t=2020-1930=90 for 2020
d=68 years (between 1930 and 1998)
R=500000%2F125000=4 is the growth factor over 68 years
(the population quadrupled in the 68 years between 1930 and 1998).
N%5B0%5D=125000 is our starting population
highlight%28N=125000%2A4%5E%28%28t%2F68%29%29%29%5Efunction, with t=yearsafter1930

PART a:
In the year 2020, for t=90, the population is
highlight%28N=125000%2A4%5E%28%2890%2F68%29%29%29%5E%28a%2Acalculation%29
highlight%28N=1782986%29%5E%28a%28approx%29%29

PART b:
To calculate when the population will be one million.
highlight%281000000=125000%2A4%5E%28%28t%2F68%29%29%29%5E%28b%2Acalculation%29
Taking logs of both sides
log%281000000%29=log%28125000%29%2B%28t%2F68%29%2Alog%284%29
From there we get highlight%28t%2F68=3%2F2%29 <--> highlight%28t=102%29,
which corresponds to year 1930%2B102=highlight%282032%29

I really did not bother with the calculation.
It was just mental math.
I knew (from way before) that the population had quadrupled in 68 years.
That meant that it doubled every 34 years,
so that in 68=34%2A2 years it would double twice,
and would end up multiplying times 2 twice to quadruple.
Then, being 500,000 in 1998,
it needed just another 32 years to double again, and reach one million.