SOLUTION: Write exact solution for 12 raised to the square root of x = 35

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: Write exact solution for 12 raised to the square root of x = 35      Log On


   

Question 678389: Write exact solution for 12 raised to the square root of x = 35
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
12%5Esqrt%28x%29+=+35
A relatively easy way to solve equations where the variable is in an exponent is to start by rewriting the equation so that each side is a power of the same number. But I don't see a way to write 35 as a power of 12 or write 12 as a power of 35 or write both 12 and 35 as powers of some third number. So this method is not available to us for this problem.

When the "easy" way can't be used, then these problems require the use of logarithms. Before you start using logarithms, try to isolate the base and the exponent (with the variable) on one side of the equation. Your equation, fortunately, already has the base, 12, and its exponent (with the variable) isolated on the left side.

Next find the logarithm of each side of the equation. Any base of logarithm may be used. But there are certain advantages to choosing certain bases:
  • Choosing a base for the logarithm that matches the base of the exponent will result in the simplest possible exact expression for the solution.
  • Choosing a base for the logarithm that your calculator "knows" (base 10, log, or base e, ln) will result in an exact expression that can more easily converted to a decimal approximation if one is needed/wanted.
Since the problem makes no mention of needing a decimal approximation we will use base 12 logarithms:
log%2812%2C+%2812%5Esqrt%28x%29%29%29+=+log%2812%2C+%2835%29%29

The next step is to use a property of logarithms, log%28a%2C+%28p%5Eq%29%29+=+q%2Alog%28a%2C+%28p%29%29, which allows us to move the exponent of an argument out in front of the log. (It is this very property that is the reason we use logarithms on these equations. The property allows us to move an exponent, where the variable is, to a place where we can "get at it" with regular algebra.) Using this property on our equation we get:
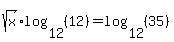
sqrt%28x%29%2Alog%2812%2C+%2812%29%29+=+log%2812%2C+%2835%29%29
By definition log%2812%2C+%2812%29%29+=+1. (This is why matching the base of the log and the base of the exponent gives us the simplest possible solution.) So this equation becomes:
sqrt%28x%29+=+log%2812%2C+%2835%29%29

To solve for x all we need to do is square both sides:
%28sqrt%28x%29%29%5E2+=+%28log%2812%2C+%2835%29%29%29%5E2
which simplifies to:
x+=+%28log%2812%2C+%2835%29%29%29%5E2
This is an exact expression for the solution. If you ever need a decimal approximation for this, then use the base translation formula, log%28a%2C+%28p%29%29+=+log%28b%2C+%28p%29%29%2Flog%28b%2C+%28a%29%29, to convert this base 12 log into a log your calculator can use (base 10, log, or base e, ln).

Here's how the solution would look if you chose base e logs instead of base 12. Since the steps are pretty much the same as the above so I will only comment on the differences:
12%5Esqrt%28x%29+=+35
ln%2812%5Esqrt%28x%29%29+=+ln%2835%29
sqrt%28x%29%2Aln%2812%29+=+ln%2835%29
This time the log on the left does not "disappear" like log%2812%2C+%2812%29%29 did. Dividing both sides by ln(12):
sqrt%28x%29+=+ln%2835%29%2Fln%2812%29
%28sqrt%28x%29%29%5E2+=+%28ln%2835%29%2Fln%2812%29%29%5E2
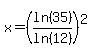
x+=+%28ln%2835%29%2Fln%2812%29%29%5E2
This is another expression for the solution to your equation. While not as simple as the solution we found above it is much easier to find a decimal approximation for this one.