Question 677060: Please verify: cos4t = 8(cos^4)t-8(cos^2)t+1
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
On the left side the argument is 4t. On the right side the arguments are just t. So we will need to use identities to change the argument from 4t to t. A formula/identity for cos(4x) is not usually taught. But cos(2x) is another matter. Usually you learn three variations of cos(2x):Looking at these equations we can see that the argument on the left, 2x, is twice the arguments on the right, x. Another way to look at it is that the arguments on the right are half's of the argument of the left. The key to learning how to use these equations effectively is to understand that they can be used to double or halve any argument. (You see how shortly.)
So we can use a cos(2x) equation to halve the cos(4t) to an expression with arguments of 2t. And then we can use the cos(2t) again to halve the argument down to just t.:


Since the right side is made of of just cos, I'm going to use the middle equation for cos(2x) since it, too, only has cos on the right:

Using cos(2x) again:

Now that the left side is expressed in terms of cos(t), just like the right side, let's simplify the left side to see what else, if anything, must still be done. First we square 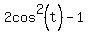 : :

Next we distribute the 2:

And add the like terms:

And, as we can see, we are finished!
P.S. To use cos(2x) to double an argument, you must have an expression that matches the pattern of the right side. For example:
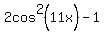
becomes
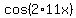
or just
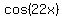
|
|
|